①桩侧摩阻力随深度的关系变化曲线为三次曲线方程z=kτ³+C,其中,z为土体深度,τ为桩体侧摩阻力.

②单元体法向位移为零且不考虑侧面剪力;

③不考虑桩体的径向变形.

当CFG桩承担上覆载荷产生向下运动趋势或位移时,桩体受到土体方向向上的侧摩阻力,称为正摩阻力.反之,当桩土之间产生沉降差,即桩相对于土体有向上运动或向上运动趋势时,则桩体受到土体提供的负摩阻力.负摩阻力与正摩阻力相等的点称之为中性点.中性点位置所对应的负摩阻力为零,在 z=0处桩体与桩间土相对位移最大,因此该处负摩阻力最大,最大负摩阻力参考Berrum 公式.摩阻力表达如下:

τ₀=Ktanφσ_s+c(1)

式中:φ为桩周土体内摩擦角,c为黏聚力,K为土体被动土压力系数,σ_s为桩间土表面竖向应力,可由文献[5]得到.

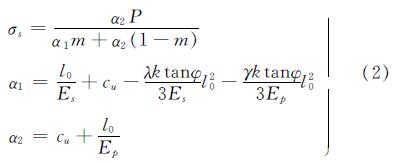
假设桩体侧摩阻力变化曲线方程为z=kτ³+C,则

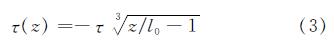
其中:l₀为中性点深度,τ(z)正值时,表示正摩阻力,τ(z)负值时,表示负摩阻力.

桩侧摩阻力随深度变化如图1所示:

图1 桩身摩阻力随深度变化曲线图
Fig.1 Diagram of friction resistance of pile body with depth

图2 桩间土微元体
Fig.2 microelement of soil between piles

σ_szA_s-(σ_sz+dσ_sz)A_s-τ(z)u_pdz=0(4)

其中:σ_sz为中性点以上某深度z₀处土体应力,A_s为单元体桩间土面积,u_p为桩体横截面周长.

令λ=(up)/(As),整理式(4),得

(dσ_sz)/(dz)+λτ(z)=0(5)

将式(3)代入上式求解,得

σ_sz=-3/4λl₀τ₀(z/(l₀)-1)^4/3+3/4λl₀τ₀+C₁(6)

将边界条件z=0,σ_sz=σ_s代入式,可解得C₁=σ_s,代回式,得

σ_sz=-3/4λl₀τ₀(z/(l₀)-1)^4/3+3/4λl₀τ₀+σ_s(7)

图3 CFG桩微元体
Fig.3 microelement of CFG pile

σ_pzA_p-(σ_pz+dσ_pz)A_p+τ(z)u_pdz=0(8)

其中:σ_pz为桩某深度z处桩身应力; A_p为桩身截面积.

令λ^'=(up)/(Ap),整理式(8),得

(dσ_pz)/(dz)-λ^'τ(z)=0(9)

将式(3)代入式(9),得

σ_pz=3/4γl₀τ₀(z/l₀-1)^4/3-3/4γl₀τ₀+C₁(10)

将边界条件z=0 σ_pz=σ_p代入式(10),可解得C₁=σ_p,代回式(10)可得:

σ_pz=3/4γl₀τ₀(z/l₀-1)^4/3-3/4γl₀τ₀+σ_p(11)

由式(7),得桩间土中性点以上变形量S_s上与中性点位置以下变形量S_s下,即

S_s上=^l0₀(σ_sz)/(E_s)dz=(3λl²₀τ₀)/(7E_s)+(l₀σ_s)/(E_s)(12)

S_s下=^l_l0(σ_sz)/(E_s)dz=-(9λl²₀τ₀)/(28E_s)(l/l₀-1)^7/3+

(l-l₀)/(E_s)(3/4λl₀τ₀+σ_s)(13)

式中,E_s为桩间土压缩模量,由于土层性质不同,取各层土的加权压缩模量,即

E_s=(E_s1l₁+E_s2l₂+…+E_sxl_x)/l(14)

式中,E_s1、E_s2、…、E_sx为各土层的压缩模量,l₁、l₂、…l_x为各土层厚度.

CFG桩在垫层中刺入深度δ1依据下式计算.

δ₁=c_u(σ_p-σ_s)(15)

c_u为桩顶作用于褥垫层的竖向刺入量.

c_u=(L_c)/(E_c)(16)

其中,L_c为褥垫层厚度,E_c为褥垫层模量.

下卧层桩端入刺深度δ₂采用下式计算.

δ₂=c_d(σ_p1-σ_s1)(17)

其中,c_d为桩端在下卧层的竖向刺入量.

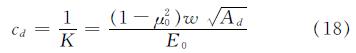
其中:μ₀为桩端泊松比,K为桩端土体的基床系数,A_d为CFG桩底面积,w为沉降影响系数,结合文献[6]取0.97,E₀为桩端土压缩模量,σ_p1,σ_s1表示桩端与桩间土.

考虑桩土协调变形,桩间土压缩量等于CFG桩身刺入褥垫层与下卧层之和,故有

S_s上+S_s下=δ₁+δ₂(19)

将式(12),(13),(15),(17)带入式(19),可解得中性点位置l₀.

由于褥垫层多为砂砾碎石构成,故不考虑褥垫层黏聚力对承载力的影响,利用太沙基承载力系数简化桩顶作用力q_u1.

q_u1=γ₁L_cN_q+γ₁dN_γ(20)

式中,N_c、N_q、N_r为承载力系数,可查阅太沙基承载力系数图得出.

N_c=(N_q-1)cotφ;

N_q=(exp[(3π/2-φ)tanφ])/(2cos²(45°+φ/2)).

N_γ=[(K_pγ/2cos²φ)-1]tanφ/2;

依据文献[6],p_u2为桩端作用力,等于桩端土的不排水抗剪强度与桩的承载力系数N_c2乘积.

q_u2=c'_u^N_c2(21)

其中,N_c2为桩承载力系数,本文取N_c2=9. 取桩体微单元体为研究对象,对桩体中性点上下部分积分,得到桩体侧摩阻力公式.

T=πd[l0lτ(z)dz-0l0τ(z)dz](22)

当桩顶先于桩端破坏时,即

q_u=q_u1+T(23)

当桩端先于桩顶破坏时,即

q_u=q_u2+T(24)

CFG桩复合地基极限承载力公式为

q_u=min(q_u1+T,q_u2+T)(25)

褥垫层厚度分别选择150、250、350、450、550 mm,其余参数参考现场试验数据.

图5 不同褥垫层厚度对中性点位置的影响
Fig.5 Effect of cushion thickness on the neutral point position

CFG桩桩径分别选择0.3、0.4、0.5、0.6、0.7 m,其余参数参考现场试验数据.

图6 不同桩径对中性点位置的影响
Fig.6 Influence of different pile diameter on the position of neutral point