基金项目:上海市住房城乡建设管理委员会科研项目(17Z44225)
第一作者:李 东(1963-),男,博士,副教授,主要从事混凝土结构裂缝控及监测研究,E-mail:Lidongbibo@163.com
(Department of Civil Engineering, Shanghai University,Shanghai 200444, China)
super-long basement-floor; temperature stress; crack control; numerical computation;
DOI: 10.15986j.1006-7930.2019.04.002
以某超大底板跳仓作业为例,分析了该混凝土底板结构跳仓施工方案设计中的主要难点,并编写了粘弹性温湿耦合有限元数值分析程序,模拟分析了施工阶段底板温度及温度应力变化情况,同时将模拟结果与实测结果进行了对比,验证了数值分析程序的准确性.在此基础上通过设置程序中的边界条件对新老混凝土接缝处的温度及温度应力变化进行了分析,并分析了跳仓间隔对新老混凝土接缝处应力释放的影响,给出了接缝处在不同种类水泥水化热影响下的应力释放规律.其分析结果可填补跳仓施工理论研究的空缺并为相似工程跳仓施工方案设计提供参考.
This paper takes the construction of a large base-plate as example,to analyze the main difficulties in the design process of the alternative construction plan. The authors developed a finite element visco-elastic numerical program coupling temperature-moisture and simulated the law of temperature and temperature stress variation about base-plate in construction. At the same time, the simulation results are compared with the measured results to verify the accuracy of the written numerical analysis program. On this basis, the temperature and temperature stress variation about the construction joints and the effect of the concrete placing time-gap on the stress release of old and new concrete joints are analyzed. The paper gives the stress release law of joints under different types of cement hydration heat. Analysis results can fill the gap of the alternative bay methods theory research and provide reference for the design of the construction scheme about similar projects.
对于超长混凝土底板结构温度裂缝控制的施工措施而言,跳仓法施工使结构一次性连续浇筑形成统一的整体是建设单位和施工方非常喜欢的一种方式.对于跳仓法的实践我国处于领先地位,然而其理论研究水平却滞后于实际工程实践,使得多数工程都依靠以往的施工经验进行跳仓施工设计,缺乏相关理论指导,其结果是造成工程质量上参差不齐,因此需要对跳仓施工中施工方案设计难点及底板的温度应力进行研究分析,由此来指导工程实践.国外对于跳仓施工法的研究鲜有涉及,而国内最早王铁梦[1]教授于1975年开始对无缝施工的跳仓法展开了实践研究,并将其运用到宝钢大型300 t氧气顶吹转炉基础的施工中,通过对其严格的温度应力计算,实现了温度裂缝控制的成功.对于跳仓法温度应力的数值分析,朱伯芳[2]教授编制了我国第一个不稳定温度场有限元分析程序、第一个混凝土温度徐变应力有限元程序等这对混凝土结构温度应力的数值计算发展起到了重要作用.张宇鑫等人[3]编制了能模拟跳仓浇筑的高拱坝温度及应力三维有限元仿真分析通用软件.赵英菊[4]应用大型有限元分析程序ANSYS,对跳仓施工阶段和施工完成结构使用阶段的温度应力进行了计算机模拟分析等等.然而现阶段对于跳仓施工过程中新老仓块接缝处的温度应力分析以及跳仓间隔变化对接缝处温度应力的影响鲜有涉及.因此本文在前人研究的基础上,通过编写粘弹性温湿耦合有限元数值分析程序并结合实际工程案例,详细论述了跳仓施工方案设计难点并对跳仓施工过程中温度应力以及接缝处温度应力作详细分析.
该项目位于上海市徐汇区为高档商业住宅,结构全长372 m,按现行规范进行设计时基础底板为超长底板,底板由地下室基坑分割墙分为东西2区,西区尺寸为88 m*201 m,东区尺寸为186 m*150 m.底板由主楼和车库底板组成,主楼底板厚1.2 m,车库底板厚0.8 m.为控制裂缝产生,底板配制双向双层钢筋.车库部分上层双向18@100,下层双向16@100,主楼部分上层双向22@100,下层双向20@100.底板混凝土强度C40,总浇筑量为3.6*104 m3.参照以往施工经验,混凝土硬化成型后残留的水化温度应力将对底板产生何种影响,以及与上部结构荷载的组合后是否引起底板的开裂均难以估计,这些影响均需在施工设计阶段进行分析.
针对现行超长结构设计,由于超长结构整体的释放变形能力较弱,按现行设计规范的概念设计,该类超限结构受荷后一定产生相应的拉伸变形,受约束势必产生相当的附加内力.该附加应力主要体现在两个方面:(1)硬化阶段,水泥水化热热产生的不均匀温度场,造成的结构内部的不均匀膨胀收缩,在内约束与外部约束共同作用下产生的温度应力;(2)服役阶段:结构受日照、温度与环境温湿变化影响产生的冷热及干湿变形,在外部约束作用下产生的变形应力.对于基础底板来讲,施工完成后受日照、温度及干湿变形的影响较小,底板的附加内力主要是硬化完成后的残余温度应力,该应力的计算和构件超长后对结构开裂产生何种影响,在设计中较难估计.设计时通常是采取各种释放变形的方法来规避或削弱这种附加内力,表1给出了设计或施工中常用的释放变形措施以及裂缝产生概率的对比[5-9].
由表1来看,仅从控裂、设计、施工、建筑功等综合角度来看,采用跳仓法一次性连续形成建筑整体结构依然是一个受欢迎的设计方案.跳仓法需要设计方与施工方共同协商完成整体结构,但该方法存在的问题是:一是跳仓施工时先期硬化的局部结构长度如何确定,一次性施工多少尺寸最好; 二是己成型和未成型构件之间的施工间歇如何确定,能够释放多少变形[10-12],《GB50496-2012大体积混凝土工程施工规范》上给出的条文也仅是经验指标.
综上该工程难点主要有三:(1)结构全长372 m,底板考虑耐久性与防水要求采用跳仓法施工,底板不设温度后浇带和温度变形缝,属于无缝超长底板;(2)跳仓分仓时先期硬化的的局部长度如何合理确定(3)规范中3~7 d的应力释放能否保证新旧混凝土接触边界不出现裂缝,具体尚未了解.
混凝土浇筑后的硬化过程是水泥浆体向固体演化的过程,此阶段内结构具有较强的蠕动性并伴有强烈的塑形变形和收缩变形,用弹性理论分析硬化阶段结构的内部应力状态不符合其物理规律,应采用粘弹性本构理论进行应力分析,其本构关系为
σ(t)=∫tτ0E(τ){α(τ)(dT(τ))/(dτ)+(d(ε∞(1-e-rsτ)))/(dτ)}*
H(τ,τ0)dt(1)
混凝土强度发展为[13]:Rc(τ)=Rc28[1+0.172 7 In(τ/28)],式中:σ(t)为粘弹性应力,E(t)为各龄期下的弹性模量,α(t)热膨胀系数,T(t)为为水化温度场,ε∞为混凝土收缩应变终值,H(t,τ0)为粘性松弛系数.将上式离散后可进行数值迭代运算.
σ(ti)=∑ni=1E(τi)·{α(τi)ΔT(τi)+
Δε∞(1-e-rsτi))}·H(τi,τ0)·Δti(2)
温度场计算主要包括发热、传导、对流三个计算步骤,由热物理平衡得到结构内部热传导方程为[2]
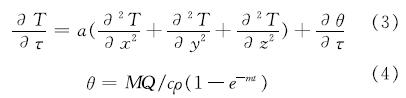
式中:α为底板导热系数; T为板内温升值; θ为水化热温升热热源函数; M为单位混凝土的水泥用量; Q为每千克水泥28 d水化热; c为混凝土比热; ρ为混凝土密度; m为水化温升速率.将结构离散为八节点等参六面体单元如图1.
由伽辽金法得到单元热传导变分方程:
式中Ni为形函数.由于水化温度随时间变化的时变性,采用接刚度法及Newmark法得到结构水化热对时间增量的方程:
([K]+([Kc])/(r·Δt)){Δt}t={F}t+(1/r-1)*
{F}t-Δt-1/r[K]{T}t-Δt(5)
{T}t={T}t-Δt-{Δt}t-Δt(6)
湿度收缩应变计算主要考虑浇筑完成后,结构与外界环境之间的湿度扩散造成的结构体积干燥收缩变化.由湿度扩散方程及伽辽金变分得单元体的湿度扩散方程为[14]
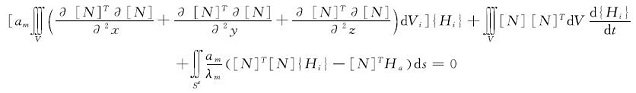
式中:am为湿度扩散系数,λm=amCm; Ha为空气相对湿度; {Hi}为湿度迁移.在单元划分基础上,由直接刚度法和Newmark法计算得到单元湿度对时间的增量方程:
([K]+([Kc])/(r·Δt)){ΔH}t={H}t+(1/r-1)*
{H}t-Δt-1/r[K]{H}t-Δt(7)
{H}t={H}t-Δt-{ΔH}t-Δt(8)
则由湿度扩散引起的混凝土体积收缩应变为
{εs}=KCm{ΔH}.
由直接刚度法得.
([K']e+[K]')·{δ}
={RT}+{R}(9)
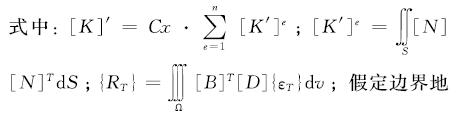
基约束为非无限刚性,由R=-Cx·U,得{R}=
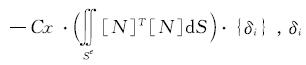
为结构在地基边界上发生的相对位移.
《GB50496-2012大体积混凝土施工规范》从经验上给出的先期硬化构件的尺寸指标为不宜超过40 m.较多工程案列超过或低于该指标都有裂缝产生,所以作者认为该指标安全可靠度不高.作者建议前期局部硬化的尺寸需通过经验计算与数值验算两种方式进行确定,前期尺寸界定及最大应力可先采用半理论半经验公式(10)与式(11)进行试算[15],然后采用本文编写的应力计算程序,验算其开裂可能性,两者交替进行从而实现尺寸的确定.
L=1.5((hE(t))/(Cx))1/2arch((|αΔT|)/(||αΔT|-|εp||))(10)
σmax=EαΔT·(1-1/ch((hE(t))/(Cx))1/2L/2)(11)
式中:E(t)为为混凝土弹性模量; h为底板厚度; Cx为地基阻力系数(混凝土管桩阻力按增加30%考虑); ΔT为综合降温差=气温差+水化热降温差+收缩当量温差; εp为混凝土极限拉应变,考虑配筋影响,按式(12)计算:
εp=7.5ft(0.1+μ/d)*10-4(Int)/(In28)(12)
式中:ft为混凝土抗拉强度标准值,C40为1.71 N/mm2; μ为配筋率0.5%; d为钢筋直径,本工程为20 mm.
局部硬化寸尺确定的流程图2所示.结合综合经验公式(10)试算结果与数值演算结果,确定的先期硬化构件尺寸为:800 mm厚底板中最大仓块为5仓66 m*31 m,1 200 mm厚底板中最大仓块为8仓67 m*15 m,均超过规范要求,具体分仓如图3所示.
底板温升曲线如图4所示,两仓水化速率一致,均在70 h左右完成水化,相应板内温度到达峰值随后开始降温,直至环境温度.8仓相对5仓板厚较厚内部热量传导及散失稍慢,温峰值和降温时刻均比5仓迟后5 h左右,同时降温速率也小于5仓.两仓温度峰值及温控情况如下:温度峰值分别为5仓58 ℃,8仓62.8 ℃; 两仓入模温升值为28 ℃左右<50 ℃; 3~7 d降温速率1.4<2 ℃/d,温控指标满足规范要求.
温度延板厚方向梯度变化如图5,最高温位于板内底面以上2/3处,高温主要分布在板的上半部分且温差较小,板下半部分温度随厚度升高近线性分布温差较大,故板上半部分温度梯度小,下半部分温度梯度大,整板的温度分布具有不均匀性,该情况将对应立及开裂造成何种影响,由应力分析得出.
底板应力分析如图6,7所示.由图5温度延板厚的梯度分布可知,升温阶段板内温度分布的不均匀性,使得底板存在一定的里表温差,内部温度高变形剧烈需要向外扩张,表面温度低变形缓慢一定程度上约束着内部的扩张,这种变形的相对差异性造成升温阶段板表面受拉,其拉应力已经超过相应龄期的拉应力标准值出现表面开裂,而内部混凝土为受压状态.降温阶段整个底板受降温差影响,表面和内部开始出现不同程度的冷缩,表面先前的拉应力受冷缩的影响逐渐降低并转为压应力,同时观察到表面裂缝缓慢消失.因此表面应力曲线可以解释,早期升温阶段出现的表面裂缝在后期降温阶段出现的“裂缝自愈”现象.内部先前的压应力受冷缩及垫层的约束逐渐转为拉应力.拉应力曲线尚未超过混凝土容许抗拉值,中部节点不会开裂.若按弹性应力σ=E(t)αΔT计算,弹性应力早在300 h左右就超过混凝土的容许抗拉强度,底板已经开裂.
5图8给出了底板早期压应力和后期拉应力在整个板厚度方向的分布情况.受压阶段最大压应力出现位置与板内最高温度出现位置具有一致性,都位于底板的中上部,且8仓温峰值偏高,压应力也相对偏高高.后期降温收缩阶段最大拉应力出现位置与早期最大压应力出现位置不同,更靠近底板的中下部,位于板底以上1/3~1/2处,而底板上部分由于底板较薄近似均匀受拉.粘弹性应力计算结果显示最大拉应力5仓为1.59 MPa,8仓为1.12 MPa,均小于抗拉强度19.1 MPa,板内部节点无开裂可能.整板截面拉应力分布较为均匀,内部与表面拉应力相近,应力值较小,无贯穿裂缝产生.为验证本文编写的粘弹性温湿耦合有限元数值分析程序计算结果的准确性性,在5仓及8仓板中分别安置温度应力传感器,采用YBY-2001型温度应力测试分析系统对该工程的5仓及8仓进行温度与应力的实测,实测结果与数值模拟计算结果对比如下图所示.
由图9温度对比结果可得出,升温阶段实测曲线与模拟曲线无显著差别,数值计算值精度较高.在降温阶段实测曲线的降温速率要明显高于模拟曲线,原因在于模拟过程中底板的表面放热系数为一定值,而实际工程中由于底板的养护时间及养护环境是变化的,因此真实情况是板的放热系数是不断变化的,这点程序是无法实现精确模拟,因此会有误差,但该误差并不影响板内最高温升及最终最大温度拉应力的模拟计算.由于本次实际施工中底板养护时间较短,在底板降温阶段养护设施撤离,因此在该阶段底板降温速率较快.由图 10应力对比结果可得出,升温阶段压应力实测曲线与模拟曲线无显著差别,误差主要存在于降温阶段,其原因仍为模拟过程中底板的表面放热系数为一定值无法准确模拟实际施工过程中表面放热
系数不断变化的情况.受本次实际施工中底板养护条件改变的影响,因此在降温阶段拉应力增长速度较快,这点与底板降温速率较快情况吻合,但底板最终最大温度拉应力的模拟结果与实测误差不大.由以上分析可知本文编写的数值分析程序虽有缺陷,但其最高温升及最大温度拉应力的计算结果与实测结果误差不大,实际工程分析中可以采用.
新老混凝土接缝处的应力状态相比于单独浇筑的仓块较为复杂,作者认为突出有两个问题:(1)是接缝作为新老混凝土的对流换热边界,其流过的热量在接缝处产生多少温升,浇筑的间隔又会降低多少温度;(2)是接缝作为新老混凝土的粘结面,新老混凝土在接缝界面上发生协同变形,引起都少应力,两次浇筑间隔又会释放多少应力.仅从力学解析去获得这两种问题的解答尚存在一定困难,更多的是通过数值计算来获得相应的解答.针对这两个问题,此次模拟中在新老混凝土边界上定义两个边界,一是对流换热边界,式(13),二是弹性约束边界,式(14).
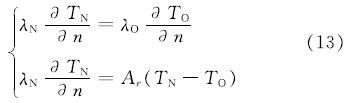
式中:λN,TN表示新混凝土的导热系数和温度场; λO,TO表示老混凝土的导热系数和温度场,新老混凝土之间热阻.
[σs]=[KO]·[Δu](14)
式中:[σs]表示接缝处应力,[KO]老混凝土刚度,[Δu]表示新旧混凝土之间的协同变形.
以浇筑间隔7 d与15 d为例,新老混凝土接缝处温度及应力变化分析如图 11.
由图 11分析知,接缝处混凝土温度变化的显著特征为经历两次升温与降温,分别是新老混凝土作为两个不同时刻的热源对接缝热传导的结果,且温度峰值最高为45 ℃小于板中温度峰值62.5 ℃.新老混凝土之间浇筑的间隔时长对第二次升温与降温有较明显的影响,由图对比分析知,第二次温峰值间隔15 d要低于间隔7 d,降低了10 ℃,第二次降温速率间隔15 d低于间隔7 d.
接缝处应力变化如图 12,显著特征是经历两次拉应力回升,两次之间存在拉压应力突变点(新混凝土发热体积膨胀对接缝挤压).第一次拉应力回升原因同底板板中(降温冷缩),拉应力强度不高不会超过混凝土抗拉标准值.第二次拉应力回升是新老混凝土在接缝处共同降温冷缩协同变形的结果,新老混凝土的冷缩拉应力在接缝处得到累加,拉应力强度较大.7 d的浇筑间隔接缝处拉应力依然达到抗拉强度开裂,应力释放不彻底.15 d的浇筑间隔使得应力得以较好的释放,接缝出应力大幅度下降小于抗拉强度,不会开裂. 为了考虑施工取材多样性,又采用不同水泥品种,模拟得到了不同跳仓间隔下接缝处的最大温度拉应力值,通过Origin作图软件绘制其最大温度拉应力散点图,并采用函数σ(t)=A·e-x/t+σ0对其进行非线性拟合,得到了接缝处应力释放规律,即接缝处最大温度拉应力随跳仓间隔延长而衰减函数方程,方程的拟合参数如表4,其中A为2.26,t为3.90,相似工程接缝处的温度拉应力分析可参考应用.由应力释放函数可计算出不同水泥品种,在保证接缝不开裂的情况下,其跳仓间隔区间取为t≥solve[σ(t),t]=ftk,ftk为混凝土抗拉强度标准值.
(1)关于跳仓作业的具体分仓尺寸应根据具体施工配合比与工程概况具体问题具体分析,在合理的经验试算与有限元验算基础上,规范中的尺寸可以突破.
(2)通过对底板的跳仓作业施工模拟发现,板内温度梯度分布直接影响板内应力的梯度分布.主要表现为板内温度梯度分布情况与拉、压应力梯度分布情况具有一致性,均为中下部梯度变化高于中上部.
(3)应力计算结果可知,底板表面应力变化与板内完全相反,表面应力曲线的变化规律可解释施工阶段表面“裂缝自愈”现象.且板中弹性应力结果显示底板过早开裂且应力值过高,与实际工程不符,准确计算宜采用粘弹性理论计算.
(4)新老底板接缝处的温度以及应力变化规律与板内完全不同,且拉应力值高于板内应力值,并且受跳仓间隔长短影响较为明显.温度出现2次升温降温,应力出现2次拉应力回升与应力突变点.第二次温升峰值与拉应力回升最大值都随跳仓间隔的增加而降低.
(5)不同水泥品种接缝应力释放对比表明,水泥品种的差别对同一底板的应力释放速率无太大影响,应力释放速率大体一致,共分为3个阶段:3~7 d内速率最快,7~15 d内速率稍低,15~30 d内速率几乎平缓.品种的差别主要体现在引起板内的应力大小上,由计算结果知粉煤灰水泥引起的板内应力最低.文中给出的不同水泥品种的应力释放函数,在相同施工工况下可以作为参考.