基金项目:广东省教育厅科研平台和科研基金项目(2017GKTSCX046); 广东省教育厅科研平台和科研基金项目(2018GkQNCX063)
第一作者:朱艳峰(1968-),女,博士,副教授,主要从事材料的力学性能研究.E-mail:1969789047@qq.com
(1.广州番禺职业技术学院 建筑工程学院,广东 广州 511483; 2.广东工业大学 土木与交通工程学院,广东 广州 51006)
Hoek-Brown强度准则; 等代圆; 应变软化模型; 声波探测; 围岩稳定性
(1.College of Civil Engineering and Architecture,Guangzhou Panyu Polytechnic, Guangzhou 511483, China; 2.Faculty of Civil and Transportation Engineering,Guangdong University of Technology, Guangzhou 51006, China)
Hoek-Brown strength criterion; equivalent circle method; strain-softening model; ultrasonic testing; stability of surrounding rock
DOI: 10.15986/j.1006-7930.2020.02.007
应用Hoek-Brown强度准则判断围岩塑性区具有很多优势,但应用起来繁琐,因此提出将Hoek-Brown强度准则的应变软化模型应用于隧道塑性区分析中,推导得到非圆形隧道的塑性区半径表达式.以重庆兴隆隧道为依托,采取四种不同的等代圆方法计算塑性区半径,并与现场声波探测结果得到的松动圈半径进行对比,发现采用Hoek-Brown应变软化模型分析围岩塑性区时计算得到结果与现场实测结果最为接近,验证了运用考虑应变软化的Hoek-Brown强度准则计算围岩塑性区半径的方法是可行的.
Applying Hoek-Brown strength criterion to judge the plastic zone of surrounding rock has many advantages, but it is cumbersome to apply. Therefore, the strain softening model of Hoek-Brown strength criterion is applied to the analysis of tunnel plastic zone, andan etpressionthe radius of plastic zone of non-circular tunnel is derived. Based on the Chongqing Xinglong Tunnel, four different equal-circle methods were used to calculate the radius of the plastic zone, and compared with the radius of the loose circle obtained by the on-site acoustic wave detection. It was found that the Hoek-Brown strain softening model was used to analyze the plastic zone of the surrounding rock. The obtained results are the closest to the field test results. It is feasible to calculate the radius of the plastic zone of the surrounding rock by using the Hoek-Brown strength criterion considering strain softening.
在弹塑性力学的理论中,对围岩弹塑性的分析计算通常采用圆形断面进行简化; 但是在实际工程中,许多隧道的形状都是非圆形,因此对于非标准圆形断面形状的隧道的弹塑性就变得十分必要.朱大勇等人基于复变函数提出了非圆形巷道的粘弹性解析解[1]; 蔡晓鸿等人根据复变函数保角变换提出了二向不等围压和内压作用下椭圆形洞室的围岩应力计算方法[2]; 非圆形隧道的弹塑性解答大多是都是基于复变函数进行计算的,计算规则复杂,不易应用.同时在分析隧道周边围岩的稳定性时,应用最多的是Mohr-Coulomb强度准则,虽然其在土体计算时吻合较好,但不能反映岩体及岩石的非线性破坏特性,而Hoek-Brown则可以描述岩体的非线性变形,充分考虑岩体裂隙及结构面信息,压力释放等因素,在描述岩体的变形方面具有明显的优势.虽然有部分学者采用Hoek-Brown强度准则[3-6],但都是基于圆形隧道断面来进行分析计算的,几乎没有将Hoek-Brown准则应用于非圆形断面隧道的弹塑性解答的; 同时绝大部分专家学者在采取岩石的峰后应力 - 应变的本构关系时也都是基于理想弹塑性模型很少采用应变软化模型来进行分析计算,而应变软化模型更能代表实际宏观观测的结果[7-8].针对以上问题,本文提出一种基于Hoek-Brown准则采用应变软化模型来对非圆形隧道断面进行弹塑性分析的简便计算方法,通过将非圆形隧道断面等效成圆形隧道断面,在MATLAB中编程来实现Hoek-Brown强度准则的应用; 对比分析在采用外接圆圆心法,大小半径之和法以及当量半径法进行等代时计算得到的弹塑性解答与现场工程实际的弹塑性解答的吻合程度,得出在工程实际中应用Hoek-Brown强度准则计算围岩稳定性时的最佳等代方法.
Hoek-Brown屈服准则由于其可以很好的反应岩石和岩体的非线性破坏特征以及结构面、应力状态对强度的影响,并且能够解释最大主应力和最小主应力对强度的影响,可延用到破碎岩体和各向异性岩体等情况,是为数不多的非线性准则之一,从而得到了广泛应用,但没有考虑应变软化区域的影响,与实际情况有偏差.本文基于Hoek-Brown准则的应变软化模型,推导圆形隧道塑性区半径的表达式,并应用于非圆形隧道.首先将模型简化为圆形断面,隧道初始应力场均匀分布.围岩发生屈服状态时满足Hoek-Brown准则:
σ1=σ3+σci(mb(σ1)/(σci)+s)a(1)
式中:σ1、σ3为第一和第三主应力,σci为岩块的单轴抗压强度; mb、s、a均为材料参数,可以通过下面公式计算得出
{mb=miexp((GSI-100)/(28-14D))
s=exp((GSI-100)/(9-3D))
a=1/2+1/6(e-(GSI)/(15)-e-(20)/3)(2)
其中:GSI为地质强度指标; D为扰动参数.应变软化模型的一个主要特点是失效准则和塑性势函数不仅取决于应力张量σij,而且取决于软化参数η; 即失效准则方程里的各个参数不是一个定值,而是随着材料的变形阶段不同而变化的,是关于软化参数η的函数.
因此本文将失效准则定义为
f(σr,σθ,η)=0(3)
在弹性阶段,软化参数η=0,对应于弹性阶段失效准则f(σr,σθ,0)=0; 当进入软化阶段以后(0<η<η*),对应于软化阶段失效准则f(σr,σθ,η)=0; 进入残余阶段后(η>η*),则对应残余阶段失效准则f(σr,σθ,η*)=0.软化参数η*通过实验测定.采用极坐标形式的应变定义软化参数η为
η=εpθ-εpr(4)
应变软化材料的本构方程通过塑性增量理论得到,而塑性增量理论可以通过塑性势函数得到,定义塑性势函数为
g(σr,σθ,η)=0(5)
根据塑性增量理论
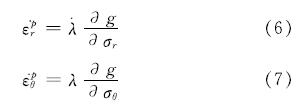
式中:λ.是一个未知的塑性乘数,式(6)~(7)是塑性阶段的本构方程,称为流动法则.目前在进行围岩弹塑性分析时认为岩体体积保持不变,而岩体在变形时体积会增大,产生扩容,对于岩体的扩容的考虑主要通过采用相关联流动法则和将扩容通过剪胀角来体现的[9],因此本文采用相关联流动法则建立采用Hoek-Brown准则应变软化模型的塑性势函数:
g(σr,σθ,η)=f(σr,σθ,η)
=σθ-σr-σci(η)(m(η)(σr)/(σci(η))+s(η))a(η)
=0(8)
其中:σθ为环向应力; σr为径向应力; σci为岩石单轴抗压强度; m为量纲为一的材料常数,用来反应岩石材料的软硬程度; s反应岩体的破碎程度,参数a用来调整失效包络曲线.在本文的所将建立的模型中,需要获取的参数为弹性阶段的弹性模量E和泊松比ν; 软化阶段参数,包括损伤模量M和剪胀角ψ和残余阶段参数η*.定义峰值参数σcp,sp,ap,mp,残余参数σcr,sr,a</sup>r,mr,,其中损伤模量M根据岩体质量和侧限应力水平求得,计算得到:
M=-ω·E(9)
其中,ω取决于峰值地质强度指标GSIpeak和侧限水平应力,可有下式计算得到
当(σ3)/((sp)1/2σci)≥0.1时,
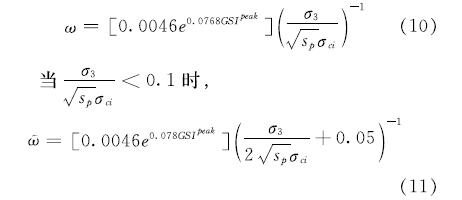
残余阶段参数即临界软化参数η*,根据公式(4)可得
η*=εp1-εp3
其中,εp1,εp3分别表示最大最小塑性应变,经过推导可得
εp1=(σp1-σr1)/E-(σp1-σr1)/M(12)
εp3=-(11+sinψ)/(21-sinψ)εp1(13)
其中,σp1和σr1分别为在某一侧压下σ1的峰值和残余值,ψ为剪胀角,本文采用HOEK和Brown提出的方法确定剪胀角即:
ψ=(5GSI-125)/(1 000)φ(14)
式中,φ为摩擦角.
假设地基材料为各向同性材料,且符合Hoek-Brown失效准则; 此时地基可视为半无限的弹塑性体.设原岩应力为σ0,在这样的地基材料中开挖一个硐室半径为 b,长度较长的地下圆形隧道结构; 并且基于这种圆形结构对围岩进行弹塑性分析,将其看作平面应变问题来求解.围岩的弹塑性分析,则就归结为弹塑性力学中的平衡微分方程、几何方程和物理方程这三大微分方程的求解,由于塑性区的解答对于围岩稳定性的影响最显著所以本文仅给出塑性区的应力场应变场及位移场的解答,计算示意图如图1所示.
其中:σ0为原岩应力; pi为隧道所加支护力; ρ表示微元半径; Rs、Rp分别表示残余半径和塑性区半径,我们将围岩应力采用极坐标表示; σr为径向应力; σθ为环向应力; εθ,εr分别表示环向应变和径向应变; 将塑性区分为 n 个同心微元圆环,并假设径向应力σr沿每个圆环均匀递减,每个微元圆环的厚度并不是相等的.对于轴对称问题,围岩在极坐标下的平衡方程可表示为
(dσr)/(dρ)+(σr-σθ)/ρ=0(15)
将上式变换应用到第i圈,列出平衡方程,根据差分法,将微分方程用微元的代数方程代替,求出近似的数值解答如下
dσr=σr(i)-σr(i-1)(16)
dρ=ρi-ρi-1(17)
在塑性区,岩石材料已经屈服,其应力状态始终满足失效准则方程(8),则第i圈的应力状态满足
σr(i)-σθ(i)=
-σci(ηi-1)(m(ηi-1)(σr(i)-)/(σci(ηi-1))+s(ηi-1))a(η)(18)
σr(i)-=(σr(i)+σr(i-1))/2)(19)
将式(15)中的半径ρ用圆环半径表示,即
ρ=(ρ(i)+ρ(i-1))/2(20)
将公式(16)~(20)带入到公式(15)中,可得
ρ(i)=
(2σci(ηi-1)(m(ηi-1)(σr(i)-)/(σci(ηi-1))+s(ηi-1))a(η)+Δσr)/(2σci(ηi-1)(m(ηi-1)(σr(i)-)/(σci(ηi-1))+s(ηi-1))a(η)-Δσr)ρ(i-1)(21)
当i=1时,则有ρ(0)=Rp
当i=n时,则有ρ(n)=b
将初始值和已知条件带入式(21),经过n次迭代和变换可求得塑性区半径Rp的表达式为
Rp=
b/(∏ni-1(2σci(ηi-1)((σr(i)-)/(σci(ηi-1))+s(ηi-1))+Δσa(η)r)/(2σci(ηi-1)(m(ηi-1)(σr(i)-)/(σci(ηi-1))+s(ηi-1))-Δσa(η)r))(22)
对于平面应变问题,对几何方程进行迭代消去位移变量得到
(dεθ)/(dρ)+(εθ-εr)/ρ=0(23)
应变由弹性应变和塑性应变两部分组成,将其表示为
εθ=εpθ+εeθ,ε</sup>r=εpr+εer(24)
将其24带入到23中得到
(dεpθ)/(dρ)+(εpθ-εpr)/ρ=-(dεeθ)/(dρ)-(εeθ)/(dρ)-(εeθ-εer)/ρ(25)
经过推导计算可得第i个圆环与第i-1个微元之间的应力表达和应变表达,表达式如下:
应力场的表达式为
{σr(i)=σr(i-1)+Δσr
σθ(i)=σθ(i-1)+H(σr(i)-,η(i-1))(26)
Δσr=(pi-σR)/n=σr(i)-σr(i-1)(27)
H(σci(η)-,η(i-1))=σci(η)(m(η)(σr)/(σci(η))+s(η))a(η)(28)
应变场的表达式为
{εr(i)=εr(i)+Δεer(i)+Δεpr(i)
εθ(i)=εθ(i)+Δεeθ(i)+Δεpθ(i)(29)
{Δεpθ(i)=
(-(Δεeθ(i))/(Δρ(i))-(1+ν)/E(H(σr(i)-,η(i-1)))/(ρ(i)-)-1/(ρ(i)-)(εpθ(i-1)-εpr(i-1)))/(1/(Δρ(i))+(1+k(i-1))/(ρ(i)-))
Δεpr(i)=-k(i-1)Δεpθ(i)(30)
{Δεeθ(i)=(1+ν)/E[-νΔσr(i)+(1-ν)Δσθ(i)
Δεer(i)=(1+ν)/E[(1-ν)Δσr(i)-νΔσθ(i)(31)
{Δσr(i)=σr(i)-σr(i-1)
Δσθ(i)=σθ(i)-σθ(i-1)(32)
k(σr,η)=
1+m(η)·a(η)·[m(η)(σr)/(σci(η))+s(η)a(η)-1](33)
Δεpθ(i)、Δεpr(i),Δεeθ(i)、Δεer(i)分别为塑性应变增量和弹性应变增量,E为弹性模量,ν为泊松比,Δρ为相邻两个微元的半径差.
经过n次迭代循环,即可求出弹塑性区域内的应力场和应变场,同时位移场也可由下列方程迭代求得:
u=εθ·ρ(34)
将上述表达式在,MATLAB环境下编程求解即可得到具体的应力应变及位移.
非圆形断面的弹塑性解答一般是通过等价圆的方式来实现的,目前常用的方法是几何等代法,也就是将非圆形断面的计算半径等代为圆形断面的应力计算半径,并带入到圆形隧道的弹塑性解答的表达式中,从而得到非圆形隧道围岩塑性区的表达式.几何等代法又包括外接圆等代法、取大小半径和的一半等代、取高度和跨度之和的四分之一等代,以及当量等代法.本文选取当量半径等代、取高度跨度之和的四分之一等代、朱合华[]等人采用方法及外接圆等代法将实际工程项目进行等代计算其塑性区半径,并与实际工程数据进行对比分析.
兴隆隧道进洞位于重庆市渝北区木耳镇良桥村,出洞位于重庆市渝北区木耳镇金岗村农业开发园区内,为双向四车道高速公路隧道,左线隧道全长2 553 m,主洞为三心圆曲墙结构,净高7.05 m,净宽10.66 m,内净空面积64.28 m2.工程区出露岩性为侏罗系中流上沙溪组砂岩,隧道断面示意图如图2所示.本次计算断面所处位置为Ⅳ级围岩,主要为中风化砂岩,岩体较完整,岩体完整性系数Kv=0.62,风化系数Kf=0.7,岩体弹性模量为5 882.8 MPa,泊松比0.17,原岩应力22.03 MPa,软化系数临界值η*=8×10-3,开挖后采用系统锚杆支护并挂设钢筋网,产生的支护压力经等效计算[10],取pi=4.8 MPa,σcp=29.6 MPa,σcr=23.3 MPa围岩基本质量指标修正值[BQ]=318,根据文献[11]查表计算可得GSIpeak=52,mi=22,D=0.23根据Hoek-Brown强度准则计算得到峰值参数及残余参数如下,mp=3.17,mr=1.41,sp=3.10×10-3,ap=0.6,sr=1.6×10-3,ar=0.505.
采用当量半径计算时当量半径r0的计算公式为[12]
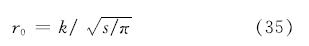
其中:k为隧道断面形状修正系数,s为面积.
朱合华等人所采用的方法计算公式为[9]
r0=[(B/2)2+h2]/2h(36)
其中:B为隧道的跨度,h为隧道高度.
采用不同方法计算得等代圆半径[13-14]见表1.
将上述四种方法所得的半径及工程参数输入MATLAB自编程序中计算得到围岩塑性区半径结果见表2.
根据现场声波探测得到现场声波示意图见图4,从图4种可以看出围岩松动圈半径为从孔口至孔深1.7 m处.在0~1.7 m声波波速随着孔深的增加而增大,随后在固定值上下波动,变化幅度减小,并逐渐趋于平缓,此时认定围岩处于未扰动状态下[15].
根据声波探测我们可以得到隧道围岩的松动圈范围,但还不能得到塑性区半径,因此通过公式(37),(38)将松动圈半径转化为塑性区半径.
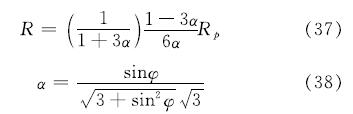
其中:φ为内摩擦角,Rp为隧道塑性区半径,R为隧道松动圈半径.通过计算可得围岩塑性区半径为1.401 m,与外接圆圆心法计算得到的计算结果偏差7.7%,与当量半径法计算结果偏差5.3%,与高度和跨度的四分之一计算法偏差12.49%,与朱合华等人的计算结果相差9.5%,由此可见,当隧道为多心圆时选择当量半径法等效计算时得到的塑性区半径与现场实测塑性区半径差距最小,由此可见,在采用Hoek-Brown强度准则计算塑性区半径时,选取当量半径法将多心圆隧道等效成圆形隧道塑性解答时准确率最高,外接圆心法次之,朱合华等人及高度与跨度的四分之一法较差.
由于修正后的模型考虑了岩石材料应变软化,且应变软化对于围岩稳定性有着重要影响,因此根据自编程程序计算得到不同计算方法下隧道围岩的残余区半径及径向位移,来分析围岩软化区域的大小,计算结果见表3,将表中数据绘制成图,从图5中可以看出在选取不同的方法计算时得到的软化区域的范围差距较大,软化区域范围竟相差20.23%之多,本文采用应变软化模型可以很好的反应材料参数随变形阶段不同而发生变化,而软化特性对于描绘岩体塑性变形具有重大影响,因此不可忽略,选取合适的等代圆计算方法对于分析围岩的应力应变及位移有很大的影响.计算得到的径向位移变化图见图6,从图6可以看出,不同等代方法下,径向位移计算结果在前期差别较大,在后期都逐渐趋于0,外接圆半径法计算得到的位移最大,应用这种方法进行设计会偏于保守,当量半径法计算得到的位移变化图居中,可以达到比较好的计算精度和工程要求.
(1)本文采用考虑应变软化特性的Hoek-Brown强度准则,在相关联流动法则下推导得出了圆形隧道应力场、应变场及塑性区半径的表达式,实现Hoek-Brown在实际工程中的简便应用,充分考虑了因塑性而引起的岩体的扩容、岩体的结构面信息及扰动情况,使计算结果更加接近围岩的实际变形.
(2)以重庆兴隆隧道为依托结合现场声波测试结果得到围岩松动圈范围,并通过公式等效计算围岩塑性区范围,通过MATLAB自编程分析在选取不同等代圆计算方法下计算得到的塑性区半径及塑性区范围发现,当隧道形状为多心圆时,应用Hoek-Brown准则分析其塑性区范围时,选取当量半径法分析得到的结果与现场实测结果相差最为接近,误差在5.3%左右.
(3)通过计算在不同等代方法下隧道围岩的位移及软化区域发现,采用外接圆法计算的得到的位移最大,采用高度和跨度的四分之一的等效方法计算得到的位移最小,而采取当量半径法计算得到的位移居中,同时发现计算半径选取的越大计算得到的软化区域范围越小,半径越小,岩体的软化特性越明显.