基金项目:国家自然科学基金项目(51978668); 广东省交通运输厅课题(DFH(201904)YS1-001)
第一作者:王文州(1967-),男,研究生,高级工程师,主要从事高速公路建设管理工作,E-mail:wwz67@126.com
(1.广东省南粤交通投资建设有限公司,广东 广州 510000; 2.中南大学 土木工程学院,湖南 长沙 410075)
隧道开挖; Hoek-Brown强度准则; 应力解; 位移解
(1.Guangdong Nanyue Transportation Investment & Construction Co., Ltd., Guangzhou 510101, China; 2.School of Civil Engineering, Central South University, Changsha 410075, China)
tunnel excavation; Hoek-Brown strength criterion; stress solution; displacement solution
DOI: 10.15986/j.1006-7930.2021.05.002
隧道开挖破坏了隧址区的应力平衡,导致围岩应力及位移场发生复杂变化,引发围岩变形过大及支护体系开裂失稳等问题,是地下工程研究的重点问题[1-2].
针对围岩应力及位移场复杂计算问题,朱艳峰等[3]提出将Hoek-Brown强度准则的应变软化模型应用于隧道塑性区分析中,推导了隧道塑性区半径表达式.陆晓清等[4]针对岩体开挖导致应力重分布问题,以深埋轴对称圆形硐室为研究对象,推导了理想弹塑性解析解.贺耕夫等[5]依据Hoek-Brown破坏准则,推导了寒区圆形隧洞理想弹塑性围岩的塑性区半径解析解.夏才初等[6]基于三维非线性Hoek-Brown强度准则,构建了考虑应变软化特性的圆形隧道开挖后围岩非线性力学响应的求解方法.文献[7-8]基于Hoek-Brown本构模型,推导了圆形隧道的弹塑性解,探讨了其适用性.Massinas等[9]在双极坐标的基础上,利用Mohr-Coulomb强度准则推导了圆形隧道围岩应力和塑性区的解析解.Exadaktylos等[10-11]推导了半圆形隧道的应力及位移计算表达式.李培楠等[12]和施有志等[13]分析了工程中常用的单心圆仰拱马蹄形隧道的解析解.程长清等[14]根据水工隧洞运行期的受力情况,运用Mohr-Coulomb与Hoek-Brown破坏准则,对无限大均质体中圆形水工隧洞在有无衬砌两种情况下的最小覆盖层厚度进行了弹塑性力学分析.
综上所述,针对服从Mohr-Coulomb准则时围岩的应力及位移解研究较多,对Hoek-Brown准则下应力及位移的求解研究较为有限,但在高围压条件下岩体节理裂隙发育,此时Hoek-Brown强度准则更合适.基于此,本文利用非线性Hoek-Brown强度准则对深埋隧道开挖产生的弹塑性区进行求解,探讨塑性区影响半径的影响因素,并对特征参数进行敏感性分析,以期为隧道开挖考虑非强度准则的应力及位移求解提供理论基础.
构建无限大均质弹性体内圆形隧道开挖问题的简化计算模型,如图1所示.
图中:σθ、σr分别为环向应力及径向应力; σ0为作用在岩土体上初始静置土压力; pi为隧道开挖边界上支护压力; r0为隧道开挖的半径; rp为隧道开挖后围岩的塑性区半径.
Hoek-Brown强度准则的屈服条件为
σθ-σr=σc(m(σr)/(σc)+S)a (1)
式中:系数m、s及a为表征岩石的基本特征的半经验参数,与参数GSI关系为
m=miexp((GSI-100)/(28-14D)) (2)
s=exp((GSI-100)/(9-3D)) (3)
a=1/2+1/6[exp(-(GSI)/(15))-exp(-(20)/3)] (4)
式(3)和(4)中D是岩石应力松弛程度或破坏程的参数,取值在0~1之间; mi取值分别为5,10,13,16和24.
轴对称问题中,岩体平衡微分方程为
(dσr)/(dr)+k(σr-σθ)/r=0 (5)
式中,k=1,2,分别为洞身和掌子面附近区域,即图1中的(a)与(b).
边界条件为: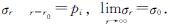
考虑轴对称问题时,弹性区中的应力和位移解为
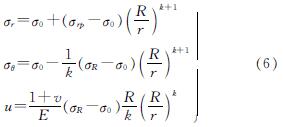
式中,R为影响区半径.
则弹塑性交界处的径向应变为
εer=-kεeθ=((1+v))/E(σR-σ0)=B (7)
将式(6)代入式(1),求得弹塑性交界处的径向应力σrp的计算表达式为
(k+1)(σ0-σR)-kσc(m(σR)/(σci)+S)a=0 (8)
式中,σ0为原岩应力.
式(8)可以通过Newton-Raphson法求解,假定初始值σr0,则
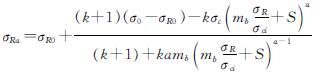 (9)
(9)
在塑性区采用非关联流动准则
hεpr+kεpθ=0 (10)
式中,参数h与剪胀角ψ有关,计算表达式为h=(1+sinψ)/(1-sinψ).
在塑性区,环向和径向总应变包括弹性应变和塑性应变两部分,表达式为
εr=εer+εpr (11)
εθ=εeθ+εpθ (12)
考虑小应变问题时,根据径向位移可求得应变表达式为

据式(10~13)中的径向位移微分方程,可得
(du)/(dr)+βu/r=f(r) (14)
式中,f(r)=εer+εeθ.
弹性塑性区交界处的径向位移边界条件为
uc=c/(2G)(p0-p1y) (15)
式中,G为围岩的剪切模量.
将式(15)代入(14),解得
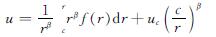 (16)
(16)
为获得式(16)的积分值,可根据弹性应变的三种形式进行求解.
(1)第一种情况
假设在塑性区中弹性变形为定值,则弹性应变表达式为
εer=-1/(2G)(p0-p1y) (17)
εeθ=1/(2G)(p0-p1y) (18)
则函数f(r)表达式为
f(r)=1/(2G)(β-1)(p0-p1y) (19)
(2)第二种情况
考虑到塑性区内壁上r=a受到内压力pi-p0的作用,外部r=c受到外部压力p1y-p0的作用,可得弹性应变为
εer=1/(2G)[(1-2v)C+D/(r2)] (20)
εeθ=1/(2G)[(1-2v)C+D/(r2)] (21)
式中,v为岩土体的泊松比;
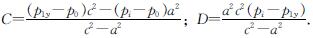
此时,f(r)表达式为
f(r)=1/(2G)[(1-2v)(β+1)C+(1-β)D/(r2)] (22)
(3)第三种情况
考虑静水压力时,弹性应变表达式为
εer=1/(2G)[(1-v)(σr-p0)-v(σθ-p0)] (23)
εeθ=1/(2G)[(1-v)(σθ-p0)-v(σr-p0)] (24)
此时函数f(r)表达式为
f(r)=2/(2G)[(1-v-βv)σr+(β-v-βv)σθ-(1-2v)(1+β)p0] (25)
根据M-C强度准则,求得函数f(r)的表达式为
f(r)=1/(2G)[D1(r/a)ar-1+D2] (26)
式中:D1=(1+β)(1-2v)(A-p0);
D2=[(1-v-βv)+αr(β-βv-v)]B.
求得式(16)中径向位移表达式为
u/r=1/(2G)1/(rβ+1)[D1f1(r)+D2f2(r)+D3f3(r)+2Guccβ-D1f1(c)-D2f2(c)-D3f3(c)] (27)
式中,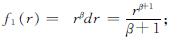
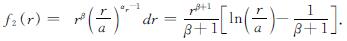
将Hoek-Brown强度准则代入式(5)中,可得
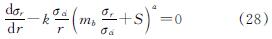
求解式(28),可得
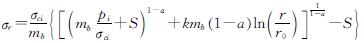 (29)
(29)
式中:r0为开挖轮廓线距离隧道中心的距离; pi为隧道支护反力.
将Hoek-Brown强度准则与式(29)联立,可获得环向应力的解析解.将σr=σR代入式(29),可求得塑性区半径计算表达式为
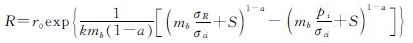 (30)
(30)
对于特殊情况k=1时,式(29)~(30)则可简化为式(31)和式(32),即
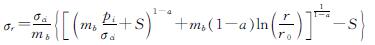 (31)
(31)
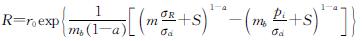 (32)
(32)
为验证本文理论的有效性与可靠性,取文献[15]的实验参数进行分析.具体为:r0=5 m,D=0.参数a、mb和S的值则根据式(2)~(4)求得,结果为:a=0.011,mb=5.128,S=0.037,其他参数如表1所示.
求解参数k为不同参数的应力值,绘制应力与塑性区半径的关系曲线,如图2及图3所示.
图2 应力与rp/r0的关系图
Fig.2 The relationship between stress and rp/r0
图2及图3表明,应力随着rp/r0的增加呈先增后减的趋势,环向应力远小于径向应力,开挖半径和rp/r0对环向应力的影响较径向应力显著.
开挖半径对塑性区半径的影响如图4所示,不同mi值时,rp/r0与隧道开挖半径的关系如图5所示.
图4表明,塑性区半径随着开挖半径的增大而增大.图5显示,当mi≤20时,rp/r0随着开挖半径的增大非线性增大; 当mi=25,rp/r0随着开挖半径的增大呈现先增后减趋势,rp/r0与GSI的关系如图6所示.
图4 塑性区半径与隧道开挖半径的关系
Fig.4 The relationship between the radius of the plastic zone and the radius of tunnel excavation
图5 rp/r0与隧道开挖半径的关系图
Fig.5 The relationship between rp/r0 and the radius of the tunnel excavation
图6 rp/r0与GSI的关系图
Fig.6 The relationship between u/r0 and GSI
图6表明,不同mi值时,rp/r0随GSI增大而非线性增大,其敏感性逐渐减弱.
利用本文推导公式,绘制u/r0随着剪胀和开挖半径的分布规律如图7所示.
图7 u/r0与剪胀系数的关系图
Fig.7 The relationship between u/r0 and the dilatancy coefficient
由图7可知,剪胀和开挖半径对u/r0的影响中,开挖半径对位移的影响更加显著.
(1)本文基于非线性Hoek-Brown强度准则,求解了隧道开挖后塑性区的应力和位移解析解;
(2)利用本文推导公式,对影响应力和位移解的多个因素进行了特征参数敏感性分析,探讨了参数间的耦合影响及作用机制;
(3)塑性区半径随开挖半径的增大而增大;
(4)应力随塑性半径的增加呈现先增后减的演化趋势,同时环向应力远小于径向应力.