基金项目:国家重点研发计划基金资助项目(2018YFC1504906)
第一作者:郭彪(1982-),男,博士,正高级工程师,主要从事地基及边坡等方面的研究工作.E-mail:gb25891775@163.com
(1.重庆市勘测院,重庆 401121; 2.云南省交通规划设计研究院有限公司,云南 昆明 650041)
(1.Chongqing Survey Institute, Chongqing 401121, China; 2.Broadvision Engineering Consultants, Kunming 650041, China)
composite foundation reinforced by stone columns; nonlinear consolidation; modulus ratio of pile to soil
DOI: 10.15986/j.1006-7930.2021.05.006
近年来,复合地基的固结问题越来越受到国内外学者的重视,取得了大量的研究成果.Yoshikuni[1]最早将复合地基应力集中效应引入到复合地基的固结理论研究中.Han and Ye[2-3]考虑了碎石桩施工的涂抹效应以及井阻作用,得到了碎石桩复合地基固结解析解.XIE K H et al.[4-5]考虑了上部荷载变化、应力在地基中的不同分布等情况,得到了碎石桩复合地基较为普遍的解析解.CASTRO等[6].考虑了桩体变形对固结的影响.LU M M等[7-8]进一步考虑了桩体内部的渗流.张玉国等[9]研究了未打穿复合地基的固结问题.
然而,由于复合地基非线性固结问题的复杂性,研究一直较少.卢萌盟[13-14]在土体与桩体压缩模量同比例增长、地基无竖向渗流、扰动区水平渗透系数不变等假设条件下得到了一个简化的碎石桩复合地基非线性固结解.显然,这些假定是不尽合理的.首先,地基存在横向及竖向组合渗流,并且土体水平渗透系数沿径向连续变化,这已经取得了共识.更为重要的是,假设在固结过程中桩土模量比不变也是与工程实际不符的.土体随着固结的进行,孔隙水排出,土体被压密,模量逐渐增大,而桩体在成桩时已经处理密实,其模量并不会随着固结的进行同步增大,相反,在较大荷载作用下,由于桩体的鼓胀变形,其模量还会有减小的趋势.也就是说,在固结过程中,桩土模量比会逐渐减小,桩土应力比也会随之逐渐减小.这对复合地基的固结有着较大的影响.基于此,本文考虑桩土模量比随固结而不断变化、地基既存在径向渗流也存在竖向渗流,土体水平渗透系数沿径向变化等因素,得到了更符合工程实际的碎石桩复合地基的非线性固结理论解答,具有较大的工程意义.
地基固结计算模型如图1所示.图中H为地基深度,re为桩影响半径,rs为涂抹区半径,rc为桩体半径,q0为上部荷载.
假设桩体的压缩性在固结过程中不变,而土体的压缩性和渗透性随着土体的固结而减小,变化符合如图2和图3所示的对数模型[10-15].
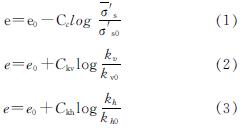
其中:Cc为土体的压缩指数、Ckv和Ckh为竖向渗透指数和径向渗透指数; 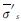 为土体某一深度处平均有效应力; σ's0为其初始值; kh为土体的水平渗透系数; kh0为其初始值; kv为土体的竖向渗透系数; kv0为其初始值; e为土体的孔隙比; e0为其初始值.
为土体某一深度处平均有效应力; σ's0为其初始值; kh为土体的水平渗透系数; kh0为其初始值; kv为土体的竖向渗透系数; kv0为其初始值; e为土体的孔隙比; e0为其初始值.
由式(1)、(2)、(3)可得土体的竖向渗透系数kv、水平渗透系数kh以及体积压缩系数mvs的表达式,即
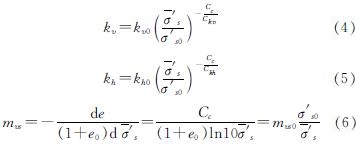
其中,mvs0为土体的初始体积压缩系数,表达式为
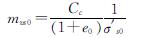 (7)
(7)
根据式(6)可得土体的压缩模量为
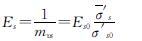 (8)
(8)
其中,Es0为土体的初始体积压缩模量.
根据图1,地基的竖向平衡方程可写成
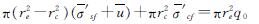 (9)
(9)
式中: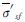 及
及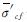 分别为土体及桩体由上部荷载产生的平均有效应力,u为土体径向的平均超静孔压.
分别为土体及桩体由上部荷载产生的平均有效应力,u为土体径向的平均超静孔压.
又由等应变条件有
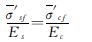 (10)
(10)
可得
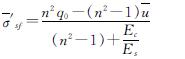 (11)
(11)
式中:Es及Ec分别为土体及桩体的压缩模量; n=re/rc.
由式(11)可得
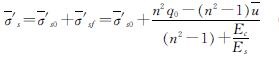 (12)
(12)
根据已有研究,地基的固结方程为[4]
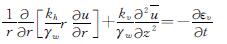 (13)
(13)
式中:u分别为土体超静孔压; εv为土体体积应变; 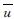 为土体径向的平均超静孔压,表达式为
为土体径向的平均超静孔压,表达式为
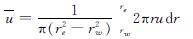 (14)
(14)
土体水平渗透系数沿径向变化,可写成
kh=kmf(r)(15)
式中:km为未扰动土体的水平渗透系数; km0为其初始值,根据式(5)有
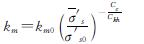 (16)
(16)
由式(13)、式(15)可得
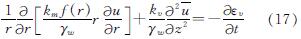
本文考虑地基顶面透水,底面不透水的一般情况.边界条件为
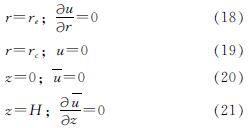
在初始时刻,土体及桩体中由上部荷载产生的有效应力 及
及 均为0,根据式(9)可得到初始条件为
均为0,根据式(9)可得到初始条件为
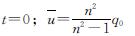 (22)
(22)
对式(17)两边对 积分,并利用边界条件(18)得
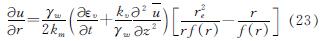
再对式(23)两边对r积分,并利用边界条件(19),得
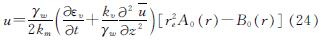
其中:
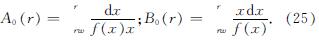
将式(24)代入式(14)可得
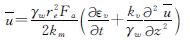 (26)
(26)
其中:
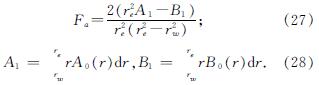
研究表明[11],涂抹区土体由于受到扰动的程度不同,其渗透性在涂抹区内是变化的,离砂井越近,扰动程度越高,土的渗透性越小,离砂井越远,扰动越小,土体的渗透系数越接近未扰动土体.本文考虑涂抹区内水平渗透系数线性逐渐变化,如图4中的模式②所示.图中模式①为传统地考虑涂抹区内水平渗透系数不变的情况.
式(27)中Fa的表达式为[13]
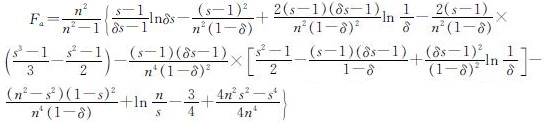
式中:s=rs/rc; δ=kr(re)/kr(rc).
又有
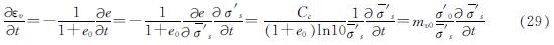
将式(4)、(16)、(29)代入式(26)可得
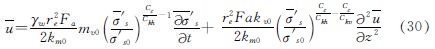
根据式(8)及式(12)可得:
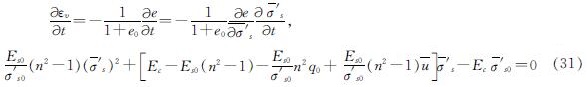
求解式(31)可得
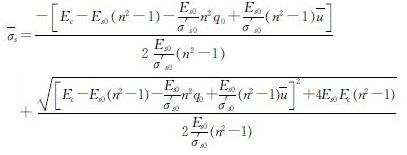 (32)
(32)
对式(32)两边求导可得:
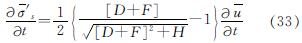
将式(32)、(33)代入式(30)可得
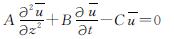 (34)
(34)
其中:
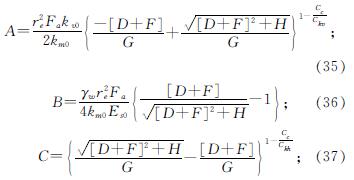
而,D=Ec-Es0(n2-1)-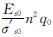 ; F=
; F=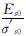 (n2-1)
(n2-1)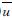 ; G=2Es0(n2-1); H=4Es0Ec(n2-1).
; G=2Es0(n2-1); H=4Es0Ec(n2-1).
为了求得问题的解析解,需要将系数A、B、C作适当简化,
参考文献[10]提出了一种简化方法,文献[12]通过室内试验进行了验证,结果显示这一简化方法是满足工程精度要求的.经简化可得:
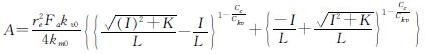 38)
38)
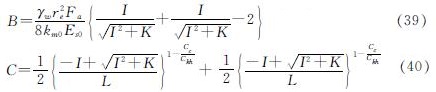
式中:I=Y-(n2-1)-(q0)/(σ's0); K=4Y(n2-1); L=2(n2-1); 而Y=Ec/Es0,为桩土初始模量比.
这样,式(34)变为关于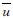 常系数微分方程,可求得其解析解.
常系数微分方程,可求得其解析解.
根据边界条件式(20)、(21),设方程式(34)的解的形式为
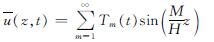 (41)
(41)
式中:M=(2m-1)/2π; m=1,2,3,….
将式(41)代入式(22),有
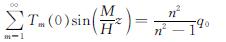 (42)
(42)
将式(42)两边乘以sin(M/Hz)后积分,可得
Tm(0)=2/M(n2)/(n2-1)q0 (43)
其中,将式(41)代入式(34)后可得
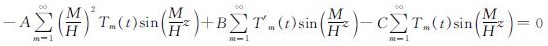 (44)
(44)
将式(44)两端乘以sin(M/Hz)后积分可得
T'm(t)+βmTm(t)=0 (45)
βm=-(A(M/H)2+C)/B (46)
又由式(45)及式(43)可得
Tm(t)=(2q0)/M(n2)/(n2-1)e-βmt (47)
将式(47)代入式(41),可得
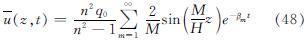
又地基的固结度为
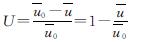 (49)
(49)
将式(48)代入式(49)可得
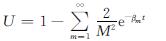 (50)
(50)
式(50)即为本文固结问题的解析解.
我们知道,在砂井地基及考虑桩土模量比在固结过程中不变的碎石桩复合地基非线性固结解中,当Cc/Ckv=1,Cc/Ckh=1时,非线性解退化为线性固结解,那么本文考虑桩土模量比随固结变化的情况是否依然如此呢?下面来探讨这个问题.
取当Cc/Ckv=1,Cc/Ckh=1时,则式(38)、(39)、(40)分别退化为
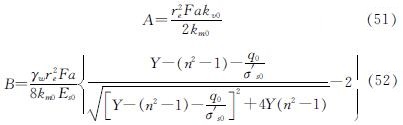
C=1 (53)
式(46)及(50)没有变化,式(46)、(50)、(51)、(52)、(53)即为Cc/Ckv=1,Cc/Ckh=1时的非线性固结解.
当不考虑地基的非线性固结时,地基的平衡方程及等应变条件可以写成
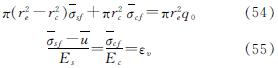
由式(53)及式(54)可得
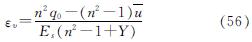
由式(55)可得
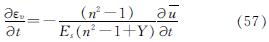
将式(56)代入式(26)并整理可得
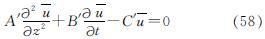
其中:
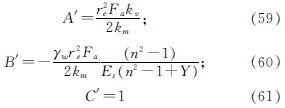
式(58)与式(34)具有相同的形式,采用相同的解答过程,可以得到不考虑非线性固结时地基的固结度为
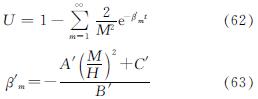
式(59)、(60)、(61)、(62)、(63)即为不考虑非线性的地基固结解.
通过对比可以看出,当Cc/Ckv=1,Cc/Ckh=1时时的非线性固结解与线性固结解并不一致,还与桩土模量比及土体初始有效应力相关.这与以往的理论是不同的.
图5是不同桩土模量比时当Cc/Ckv=1,Cc/Ckh=1时的非线性固结解与线性固结解的比较,计算参数为n=4,s=2,H/rc=40,kv0=2,δ=0.4,q0/σ's0=5.从图可以看出,当Cc/Ckv=1=1,Cc/Ckh=1时,地基非线性固结度与线性固结度并不相等,而是地基非线性固结比线性固结要慢,并且桩土模量比越大,两者差距越大,当Y=20时,最大相差约18%.
图5 不同桩土模量比时本文解与线性固结解的比较
Fig.5 Comparisons between the present solution and the linear consolidation solution for different modulus ratios of pile to soil
图6是不同荷载初始应力比时当Cc/Ckv=1,Cc/Ckh=1时的非线性固结解与线性固结解的比较,计算参数为n=4,s=2,H/rc=40,km0/kv0=2,δ=0.4,Y=10.从图可以看出,当Cc/Ckv=1,Cc/Ckh=1时,同样地有地基非线性固结比线性固结要慢,并且荷载初始应力比越大,两者差距越大.当q0/δ's0=10时,最大相差约13%.
图6 不同荷载初始应力比时本文解与线性固结解的比较
Fig.6 Comparisons between the present solution and the linear consolidation solution for different ratios of load to initial stress
碎石桩复合地基的非线性固结性状在已有文献[13-14]中进行了较多的论述,在这里不再赘述.与已有研究相比,本文对碎石桩复合地基的非线性固结主要有以下几点改进完善:一是考虑桩土模量比在固结过程中是变化的,这是本文的核心创新点; 二是既考虑了地基的径向渗流也考虑了地基的竖向渗流; 三是考虑了水平渗透系数径向变化.通过改进,使得本文解析解更加符合工程实际,有较好的理论及工程意义.下面针对上述几点对地基的非线性固结进行分析.
图7(a)、7(b)是本文解与考虑桩土模量比不变情况下解的对比情况.图中Cc/Ck表示Cc/Ckv及Cc/Ckh.
图7 本文解与考虑桩土模量比不变情况下解的对比
Fig.7 Comparison between the solution in this paper and that considering the invariable modulus ratio of pile to soil
图7(a)的计算参数为n=4,s=2,H/rc=40,km0/kv0=2,δ=0.4,q0/σ's0=5,Y=10.图7(b)的计算参数为n=4,s=2,Hrc=40,km0/kv0=2,δ=0.4,q0/δ's0=5,Cc/Ckv=Cc/Ckh=5.可以看出,本文考虑桩土模量比随固结变化情况下的解比假设桩土模量比不变情况下固结要慢,并且Cc/Ckv越小,桩土初始模量比越大,两者差距越大.在图7(a)中两者最大相差约14%,在图(b)中两则最大相差约13%.这是由于假设桩土模量比不变时,桩体模量随固结增大,高估了桩体分担的荷载而低估了土体承担的荷载,因此高估了地基的固结度.另外,从图可以看出,Cc/Ck越大,地基固结越慢,桩土模量比Y越大,地基固结越快.
图8是本文解与忽略竖向渗流情况下解的对比情况.计算参数为n=4,s=2,δ=0.4,q0/σ's0=5,Y=10,Cc/Ckv=Cc/Ckh=5.可以看出,忽略竖向渗流时固结最慢,km/kv越小,H/re越小,本文解与忽略竖向渗流时差别越大,不过总体差别均不大,均在6%以内,这说明碎石桩复合地基以径向渗流为主.
图9是本文解与考虑地基扰动区水平渗透系数不变时解的对比情况.计算参数为n=4,H/rc=40,km0/kv0=2,δ=0.4,q0/σ's0=5,Y=10,Cc/Ckv=Cc/Ckh=5从图可以看出,地基扰动区范围越大,地基固结越慢; 本文考虑地基扰动区水平渗透系数线性变化比认为水平渗透系数不变要快,在本图中,两则最大相差约10%.
本文针对碎石桩复合地基非线性固结问题,考虑桩土模量比随固结逐渐变化、地基径向及竖向组合渗流、涂抹区土体渗透系数线性变化等复杂条件,得到了更加符合工程实际的地基非线性固结解析解.并对解进行了验证,对地基固结性状进行了分析,得到以下主要结论:
(1)在考虑桩土模量比随固结而不断变化情况下,当Cc/Ckv=1、Cc/Ckh=1时,地基非线性固结解与线性固结解不相等,还与桩土模量比及土体初始有效应力相关.这与以往的理论是不同的;
(2)本文考虑桩土模量比随固结变化情况下的解比假设桩土模量比不变情况下固结要慢.因此如果忽略桩土模量比在固结过程中的变化会高估地基的固结度;
(3)考虑地基扰动区水平渗透系数线性变化比认为水平渗透系数不变固结要快,传统理论假设扰动区水平渗透系数不变偏于保守.