基金项目:云南省重点研发计划基金资助项目(社会发展领域)(No.2018BC008)
第一作者:魏德永(1993-),男,硕士研究生,主要从事岩土工程方面的研究工作.E-mail: 396431183@qq.com
通讯作者:阮永芬(1964-),女,教授,主要从事岩土工程方面的教学及科研.E-mail:ryy64@aliyun.com
(1.昆明理工大学建筑工程学院,云南 昆明 650500; 2.中铁三局集团广州公司,广东 广州 510000)
(1.Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China; 2.Guangzhou Company of China Railway Third Bureau Group, Guangzhou 510000, China)
geotechnical parameters; Bayes large sample method; improved Bayes-Bootstrap method; minimum sample siz; foundation pit excavation
DOI: 10.15986/j.1006-7930.2021.05.013
由于在岩土工程中存在大量的不确定和不确定性因素,应用可靠性理论解决岩土工程中的问题一直比较困难,但有很好的应用前景[1].
土工试验后采用经典统计学方法给出岩土参数值.在岩土工程分析中一般认为:若样本量n≤38,即可认为是小样本[2].Keaton JR[3]王桂林[4] 、朱焕珍[5] 、苏永华[6] 、Luis-Fer nando Contreras[7-8] 、阮永芬[9]等采用经典统计学方法和Bayes法去推断岩土参数,并取得很好的成果.
文献[9]指出在nmin=200时,土的力学参数收敛效果已经很好.但一般工程由于样本量的限制,导致样本信息不能很好地反应土层的总体信息时,有必要在原样本的基础上采取相应的数学方法对样本量进行扩大.因此,本文在所收集土体样本c、φ不足200时,采用基于插值法改进的Bayes-Bootstrap法去扩充样本,保证每种土的样本量n都达到200以上,然后采用文献[9]的方法推算Bayes大样本法下的岩土后验分布以及先验分布的超参数值,得出后验分布表达式以及收敛值,再求出后验分布在风险最小情况下的岩土参数可靠区间.随后根据后验均值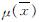 与样本均值
与样本均值 和样本量n之间的关系反算岩土参数达到可靠值时所需样本量的最小量.并通过一个基坑开挖工程,结合开挖过程中的深层水平位移的实际监测数据和改变参数情况下的有限元模拟深层水平位移数据进行对比,验证Bayes-Bootstrap法确定参数的可行性.
和样本量n之间的关系反算岩土参数达到可靠值时所需样本量的最小量.并通过一个基坑开挖工程,结合开挖过程中的深层水平位移的实际监测数据和改变参数情况下的有限元模拟深层水平位移数据进行对比,验证Bayes-Bootstrap法确定参数的可行性.
对滇池湖湘沉积的特殊软土如泥炭质土、粉土及黏土等力学指标c、φ进行收集,因为岩土参数会随取样场地不同而存在较大的变异性[1],故把数据收集范围局限在昆明滇池会展中心,分地层对参数进行收集及相关计算.
对收集的样本,采用宫凤强[10]等提出的同时考虑峰度和偏度的方法对参数进行调整,调整后的样本量作为先验信息作出样本频率直方图如图1所示.根据张继周[11]等提出的方法,把岩土参数视为随机变量,确定了样本分布的最佳概率分布类型,检验结果如表1.从图1和表1可看出,三种土c、φ的先验分布都符合N(μ,σ2)正态分布,μ、σ分别为均值及方差.
图标 变异系数 偏度系数绝对值 密度函数类型a 0.199 0.015 89 正态分布b 0.267 0.023 64 正态分布c 0.258 0.016 38 正态分布d 0.208 0.022 41 正态分布e 0.316 0.027 14 正态分布f 0.018 0.024 58 正态分布
由图1可知三种土的力学参数样本量最大的为粉土,n=90; 泥炭质土的最小n=66.与文献[9]相比样本量还较少,因此需对岩土参数进行扩充,使样本量n≥200.骆飞[12] 、孙慧玲[13-14] 、何成铭[15]等对Bayes- Bootstrap法下的数据的重构提出了不同的方法.综合对比各种方法下的数据重构,最后发现基于插值法改进的Bayes-Bootstrap法比一般的Bayes法或者Boot- strap法的数据重构不仅存在效率较高,而且也能逐步扩展到取样之外的样本信息的优势.故本文把勘察得到的小样本作为先验信息,基于插值法改进的Bayes- Bootstrap法对样本进行扩充.方法如下:
设x1,x2,x3,…,xn是从某层土的总体样本中随机抽取的有限样本,并将这些样本按照某一步距h随机分为k组(h,k都为整数),其中h=n/k.每组样本里有h个数据,B1=(x1,x2,…,xh),…,Bk=(xk,xk+1,…,xn ).其中k=n-h+1.则样本量矩阵为

此时仅对原样本分组,样本容量没有得到改变.改变样本量的方法是对每组数据进行从小到大排序:
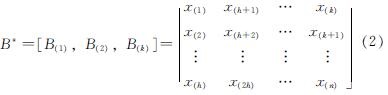
对x(i)的观测值的做邻域可得
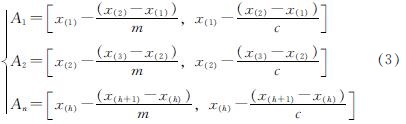 (3)
(3)
经笔者试算取不同的m值时采用式(3)扩展形成的样本与原始数据的相似度很高,不足以表征地层的总体信息,因此把式(3)加以改正,采用另外一种方式去对样本量进行扩展,如式(4).
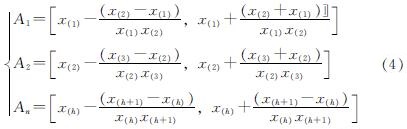
此时x(0)便可从式(5)中确定(取区间的左端点值):
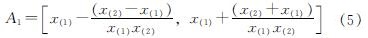
x(h+1)从式(6)中确定(取区间的右端点值):
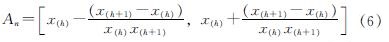
每次计算结束后样本增加2个,之后对第2组到第k组的样本量进行重复操作,完成之后样本总量扩充为n1+2k个,依次重复上述步骤,直至样本达到各个参数的样本量n≥200.之后做出各个参数样本频率直方图如图2.同理可做出K-S检验表,也能验证图2也是符合正态分布的.但限于篇幅问题,不再一一列举.
从图1和图2可知,岩土力学参数的先验与后验分布基本都符合正态分布,在得到先验信息与样本信息分布之后根据文献9所提供的方法计算后验超参数,以确定后验分布表达式,文献[2]也指出在样本分布为N(μ,σ2)的正态分布时,样本的后验分布为服从t(vn,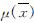 ,σ2n/kn)参数的一元t分布,vn,
,σ2n/kn)参数的一元t分布,vn, ,σ2n/kn为后验的超参数,具体计算方法参见文献[9].相关参数计算后归入表2.
,σ2n/kn为后验的超参数,具体计算方法参见文献[9].相关参数计算后归入表2.
表2中n0、μ0、σ0和n、μ、σ分别为先验分布图1中及改进Bayes –Bootstrap扩展后的分布图2中样本的样本量、均值和标准偏差.得到超参数后,通过MATLAB做出三种土六种参数的先验、样本、后验分布图,如图3.
从图3可以看出,三种土六个参数的先验分布与样本分布的形式基本一致.因为在数据重构过程中某个值的频率如果很大,该值在数据重构时所占比重会很大,故先验分布与样本分布均值很接近,一定程度上对原始先验样本的依赖性较高,故两者的相似性较高.另外随着样本增加参数均值也是逐渐收敛的,也说明岩土参数不需要达到200以上,仅需要一个合适的样本量,此时既能得到准确的参数取值,也可节约成本.另外比较三种土c的后验分布都较先验分布、样本分布集中,取值更加方便; 而三种土φ的后验分布则表现出与样本和先验分布之间区别不是很大,从表1可知三种土φ的先验与样本分布中标准偏差σ2都较小(最大为1.77),故数据间的离散性不是很强,导致Bayes大样本法的后验分布与样本和先验分布相比的效果不是很明显,尤其4-0-0层粉土φ的(σ2=0.34)后验分布的拟合效果远不及样本和先验分布,但是由于样本的增加,最大后验分布密度可信区间是在减小的,这与分布的形式无关.图3也在一定程度上说明了样本的增加,确实可更准确、更方便地确定岩土参数的取值.随着样本的增加,各地层参数取值是逐渐收敛的,但是样本应该取为多少?也就是说没必要把样本量勘察很大,需要一个合理的样本量,它既能节约成本,又能带来准确的地层信息.
通常情况下一个区间的选择是否合理,区间的精度即区间长度是可以通过可信度1-α来反应的.理论上区间可信度1-α越大,区间越短效果越好.通常寻找最优可信区间的方法是给定一个α,控制可信度(本文中α=0.05,即可信度为95%),寻找长度最短的区间.通常可获得的可信度为1-α的区间不止一个,但必定会有一个是最短的[2].等尾可信区间[16]在实际中应用较为广泛,且计算方便,但是不是最好的,即区间长度还不是最短.若后验分布是单峰对称,则等尾可信区间是最好的.要使可信区间最短,并且把后验密度的点都包含进去,而在区间外的点的后验密度值都不会超过区间内的点的后验密度值,这样的区间就称为最大后验密度可信区间,如图4所示.
样本足够大时,参数μ后验分布可用一个与先验分布无关的分布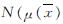 ,I-1n(μ))来代替[9],其中
,I-1n(μ))来代替[9],其中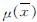 为大样本情况下后验分布均值,I-1n(μ)为其观测Fisher信息量的倒数,在后验分布为一元t分布时:
为大样本情况下后验分布均值,I-1n(μ)为其观测Fisher信息量的倒数,在后验分布为一元t分布时:
I-1n(μ)≈(σ2n)/(kn) (7)
其中,kn=n+k.
此时参数μ的最大后验密度可信区间为
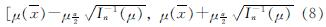
式中:μα/2为标准正态分布N(0,1)情况下上侧分位数,α=0.05时取1.96.岩土力学参数在工程中采用标准值[1],标准值可以采用下式确定.
μk=γsμ (9)
式中:μk为土体参数标准值; γs为统计修正系数,即
γs=1±((1.704)/(n1/2)+(4.678)/(n2))σ/μ (10)
考虑到不利组合,对于抗剪强度指标γs取负号[1],式中n、μ、σ分别为Bayes –Bootstrap扩展后的样本分布图3中样本量、均值和标准偏差.据此就可得到三种土c、φ的最大后验密度可信区间、标准值、经典统计学区间等,如表3.
从表3中可直观地看出三种土的力学参数的标准取值都在最大后验密度可信区间与典统计学区间内,并且与最大后验密度可信区间的差距更小.经典统计学区间长度总体比最大后验密度可信区间长,过于保守,因其上限值都比最大后验密度区间大,下限比最大后验密度区间小.最大后验密度区间较短,在参数的取值上比经典统计学的取值更加方便,在此证实了Bayes大样本方法的实用性.值得指出的是:4-0-0层粉土φ样本分布的标准偏差虽然很小,但在同一置信水平下经典统计学区间还是比Bayes大样本最大后验密度可信区间长,这是因随样本量增多时,从获得的样本中可观测到费希尔信息量I(μ)也会逐渐增加,对样本总体分布情况的掌握度会更全面,导致I-1n(μ)会减小,区间长度变得较短.这也在一定程度上说明了最大后验密度可信区间与分布的形态无关,主要取决于所勘测到的样本信息值.
随着样本数的增加,样本的特征参数值是逐渐收敛的.但要获得大量数据,需要花费巨大成本,统计分析的目的就是在花费成本与可靠值之间寻找一个平衡点,力求最小费用情况下获得最准确参数.
传统的经典统计学方法指出,确定岩土参数的取值时,样本一般取件不超过20件,但是这样岩土参数概率分布的特征参数是否收敛,这值得考验,因此本文从大样本角度论述了岩土参数取值达到收敛时所需的最小样本量并给出建议值.
土体的变异系δ由下式确定:
δ=σ/μ (11)
式中,μ、σ分别为样本分布均值及标准方差.
计算出各土层参数的变异系数、各参数在样本趋于无穷时参数的最后收敛值及该值在95%可信区间内的变动范围作为土体强度参数的包络线,为寻找样本数量时提供参照标准.
从图2知当样本量达到500时,参数变异系数δ很小,并已保证岩土参数μ是收敛的.实际上大样本情况下岩土参数样本趋于无穷时岩土参数的收敛值就近似等于后验分布中t分布的位置参数μ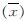 的值,据此可寻找最小样本量,让力学参数均值达收敛值附近.
的值,据此可寻找最小样本量,让力学参数均值达收敛值附近.
当得到岩土参数趋于无穷时的收敛值,反过来寻找样本量最少应该为多少,才能得到表征地层信息的合理参数取值.在样本趋于无穷时岩土参数收敛值近似等于后验t分布中位置参数 为
为
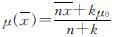 (12)
(12)
式中: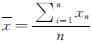 ,k=λ/(2σ),k、λ为后验超参数; μ0为先验信息均值.
,k=λ/(2σ),k、λ为后验超参数; μ0为先验信息均值.
在样本量为200时,岩土参数是收敛的,故式(12)中的μ0、k、λ等参数可以保守地取表2中的值.此时 对(12)式取极限为
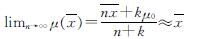 (13)
(13)
式中: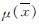 为后验均值; n为样本量; k、λ为先验超参数,因为本文已经从大样本的情况下论证了岩土力学参数在本文的样本量时是收敛的,故而k、λ可以保守地取表2的中的值.
为后验均值; n为样本量; k、λ为先验超参数,因为本文已经从大样本的情况下论证了岩土力学参数在本文的样本量时是收敛的,故而k、λ可以保守地取表2的中的值.
据式(13)便可绘出样本量与收敛值间的关系.以泥炭质土φ为例,为了与经典统计学方法比较,也在同一个图中标注了经典统计学方法的95%及Bayes法的最大后验密度的可信区间为其包络区间,为寻找合适的样本量提供依据,如图5所示.
由图5清晰可见,采用经典统计学方法确定的95%最大后验密度可信区间比Bayes法确定的宽,这是过于保守的.在参数取值上来说,一定程度上Bayes法比经典统计学方法更具优势,但从取样样本角度来看,经典统计学方法又比Bayes方法更具优势,从图5可知,经典统计学方法达到样本量为95%的可信区间时,所需要的样本量仅仅只需要10个左右,而Bayes方法达到最大后验密度可信区间的范围则需要40个左右.泥炭质土φ的样本选取上本文提取到了66个(图1b图),但是采用Baye s-Bootstrap扩充后样本为500个(图2b图)故扩充后的样本是远远大于Bayes法的最大后验密度可信区间个数的,本文确定的参数取值是能代表本地层实际情况的,也是可以为小样本
方法提供检验的.同理可做出其余土体指标的收敛值和样本量的关系图,从而确定个土体指标达到收敛值时的最小样本量.同时将经典统计学方法以及Bayes法下的标准值收敛值等整理归入表4中.
由图5和表4可知,岩土力学参数后验均值μ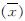 开始时随样本量的增加也在不断波动,当样本量到达某个值时,后验均值
开始时随样本量的增加也在不断波动,当样本量到达某个值时,后验均值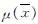 逐渐稳定下来,且不再随样本的变化而变化.本文采用的样本量是远远大于所需最小样本量,故计算结果能很好地体现地层的总体信息,为小样本方法提供检验,有很好的工程意义.
逐渐稳定下来,且不再随样本的变化而变化.本文采用的样本量是远远大于所需最小样本量,故计算结果能很好地体现地层的总体信息,为小样本方法提供检验,有很好的工程意义.
Bayes法所确定的收敛值和标准值与经典统计学方法所确定的方法是不同的,为了检验何种方法确定的参数取值的准确性更高,以昆明某地铁基坑开挖过程为案例,结合开挖过程中的监测数据,通过maids-GTS NX有限元软件对基坑开挖过程进行模拟,代入不同方法下确定的土力学参数模拟计算开挖过程中基坑深层水平位移的变化,并和实际监测数据对比分析,以验证方法的可行性.
滇池卫城站位于环湖东路与红塔东路交叉口的西南象限.地表以下依次分布着广泛的素填土、泥炭质土、粉土、黏土等.具体开挖顺序如图6:
通过对勘察报告的数据整理,结合本文的算法得出滇池卫城基坑各个地层的Bayes法收敛值以及经典统计学方法c、φ的标准值,采用参数见表5和表6.
表5 基坑开挖模拟分析时不同地层岩土参数指标取值
Tab.5 Values of geotechnical parameters of different strata in foundation pit excavation simulation analysis
拟建车站为地下二层岛式车站,车站主体总外包长度为205.9 m,端头井段外包宽度25.5 m,基坑深度标准段深度18.49~18.86 m,端头井段19.19~21.58 m.
拟建工程围护结构采用地下连续墙与内支撑相搭配的围护体系,其中地下连续墙采用800 mm厚的墙体为围护结构.基坑第一道支撑采用800×800现浇钢筋混凝土支撑,支撑在冠梁上.其他三道支撑为Φ800,t=16 mm的钢支撑,支撑在连续墙上.地下连续墙、冠梁、混凝土支撑、混凝土角撑、导墙采用C30混凝土.钢筋采用Q235.施工工序如图6所示,围护结构布置及断面选择如图7.
图7 基坑深层水平位移监测点布置和断面选择图
Fig.7 Layout of monitoring points and section selection for deep horizontal displacement of foundation pit
力学参数的本构模型的选择对计算结果也影响较大.修正摩尔库伦准则能模拟包括软土和硬土在内的不同类型的土体行为的双硬化(压缩硬化和剪切硬化)弹塑性模型,它考虑了土体的剪胀特性,引入了屈服帽盖,土体刚度随应力变化而变化,与实际情况更加符合,故本文参数的本构模型为修正摩尔库伦模型.
根据实际情况选取监测数据比较全面的6个监测点断面进行有限元建模分析,监测点布置及断选择如图7所示.本基坑开挖深度H=16 m,因基坑左右两侧3倍深度范围内影响较大,故基坑左右各取50 m,深度方向取围护地下连续墙深度的2倍,取60 m,按照土层信息对地层进行划分共计50 468个节点,基坑网格模型如图8所示:
如果规定图9中红色部分表示开挖过程中基坑深层水平位移方向向右为正,则左侧蓝色部分为负,两者数值接近,变形方向不同则颜色也不同.通过提取得到不同开挖阶段基坑个某点的深层水平位移、地表沉降等数据与实际监测结果对比,如图 10所示.
从图 10可以看出,基坑水平位移的有限元计算结果与实际监测结果相比有如下特点:有限元计算曲线与实测曲线发展规律基本一致,均表现为中间部分最大,两头较小,在深度26 m范围内,三种曲线的最大值基本出现在相同的位置处;
模拟结果均比实测结果小,用经典统计学方法确定的结果计算所得的水平位移最小,Bayes方法次之.但Bayes法计算值模拟所得的结果与实际监测情况更加接近.
本文从Bayes大样本统计法角度出发,采用Bayes -Bootstrap法对勘察所得小样本进行模拟抽样并且对样本进行扩充,分析岩土参数的收敛取值,并反过来给出达到参数收敛时的最小样本量,以一个实际基坑工程为例,对所得参数进行检验,可得出主要如下结论:
(1)岩土参数在小样本时,把勘察样本加以修正可作为先验信息.样本不足时可通过基于插值法改进的Bayes-Bootstrap法对样本进行扩充,结合先验分布,样本分布推导的后验分布,得出的最大后验密度可信区间比经典统计学所得区间更窄,c、φ的标准值就落在最大后验密度可信区间内.且最大后验密度可信区间与分布的形式无关,样本量越大,对样本总体的认识越充足,最大后验密度可信区间越窄,取值越方便;
(2)当样本量增加,岩土参数的收敛值逐渐向后验均值 靠近,先验分布的影响逐渐减小,误差数据逐渐被洗去;
靠近,先验分布的影响逐渐减小,误差数据逐渐被洗去;
(3)Bayes法所确定岩土参数取值区间较小,但是所需样本量较大.而经典统计学法给定岩土参数区间较大,精度不高,所需样本量较少.用Bayes法所确定的参数取值在基坑开挖时基坑深层水平位移明显比用经典统计学方法确定取值效果好,Bayes法的计算结果与实际结果更加吻合.