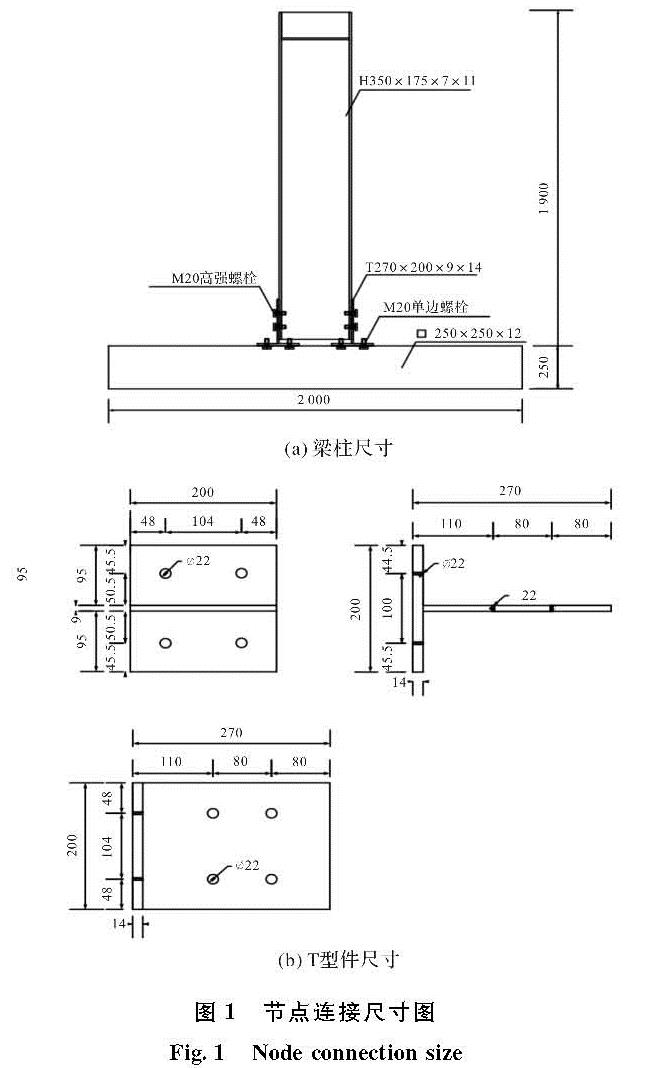
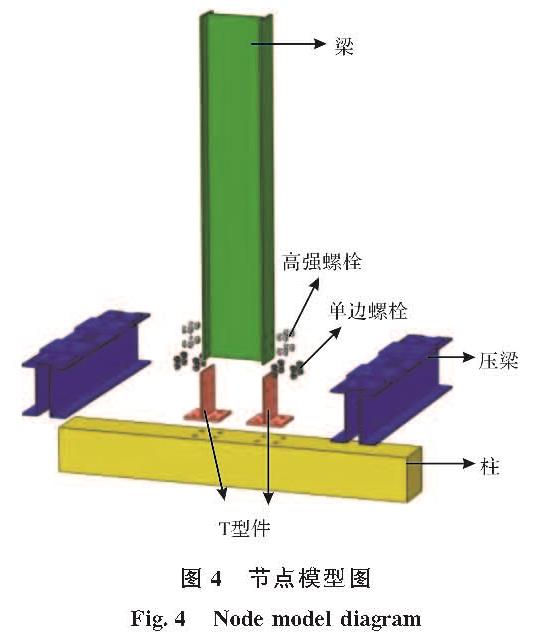
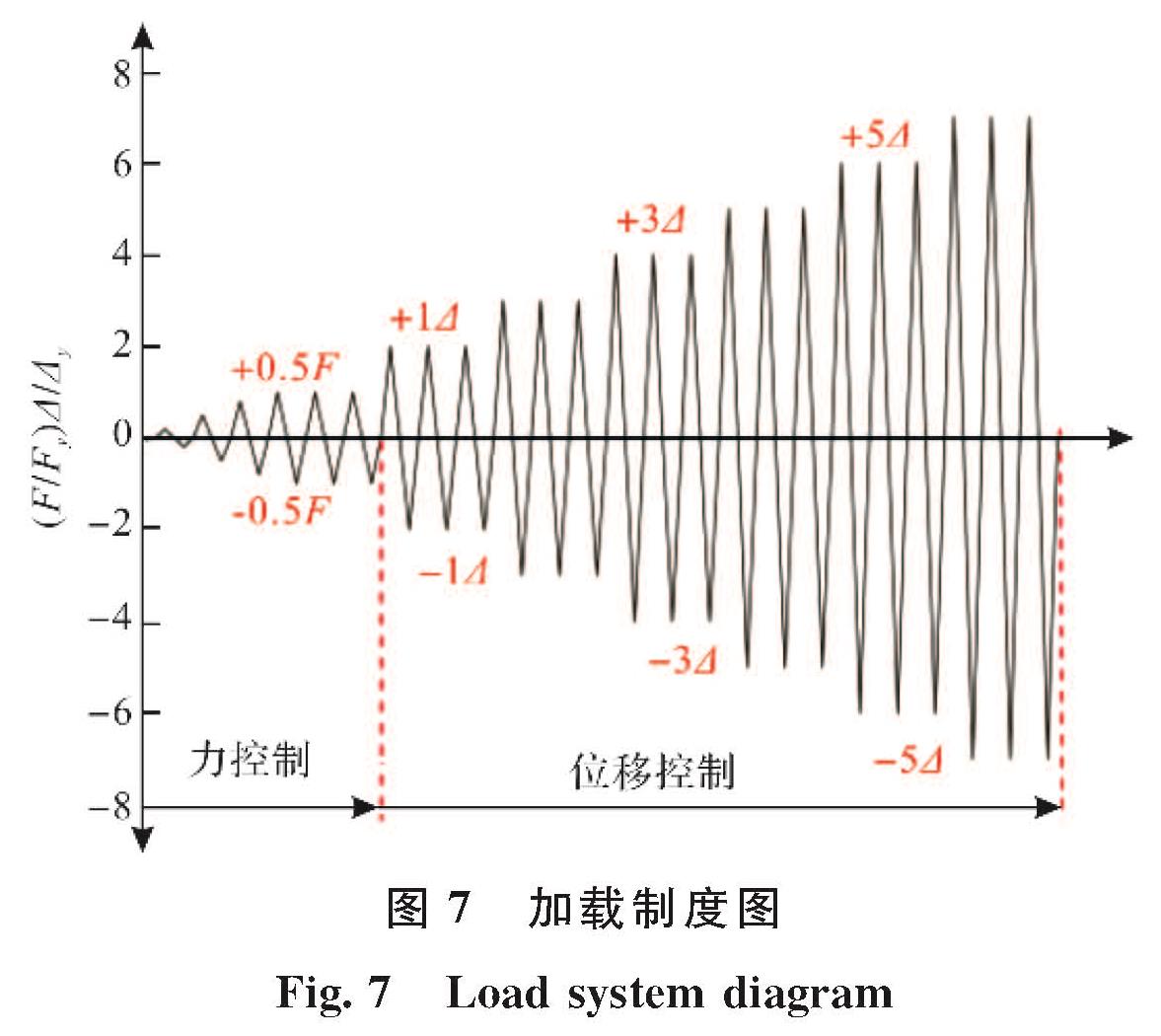
3.1 试验结果
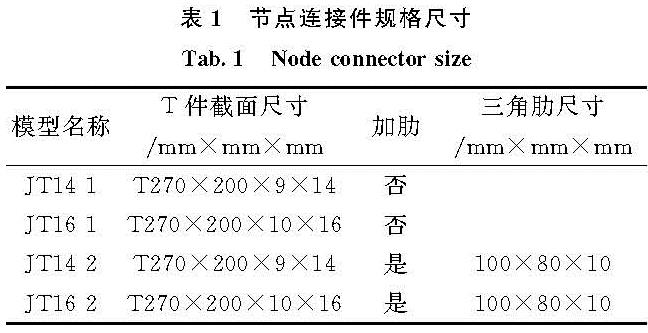
四个试件的试验结果如表3所示,分析可知:改变T型件的厚度或者加三角肋板对构件的极限位移和承载力均有不同程度的影响.(1)增加T型件翼缘厚度,JT16-1比JT14-1的极限荷载提升了28.94%,梁端极限侧移有很大变化,提升了101.10%;(2)在T型件厚度同为14 mm的情况下,加肋板的JT14-2比不加肋板JT14-1的极限承载力和梁端极限侧移分别提升了31.28%、37.83%;(3)JT16-2比JT16-1在T型件翼缘厚度16 mm条件下加肋梁端承载力和极限位移有比较明显的变化,分别是13.28%及-6.11%;(4)JT16-2比JT14-2在同时加肋的状态下,改变其翼缘的厚度,承载力和梁端极限侧移提升了11.27%及37.01%.
表3 试验结果
Tab.3 Experimental data
3.2 滞回曲线
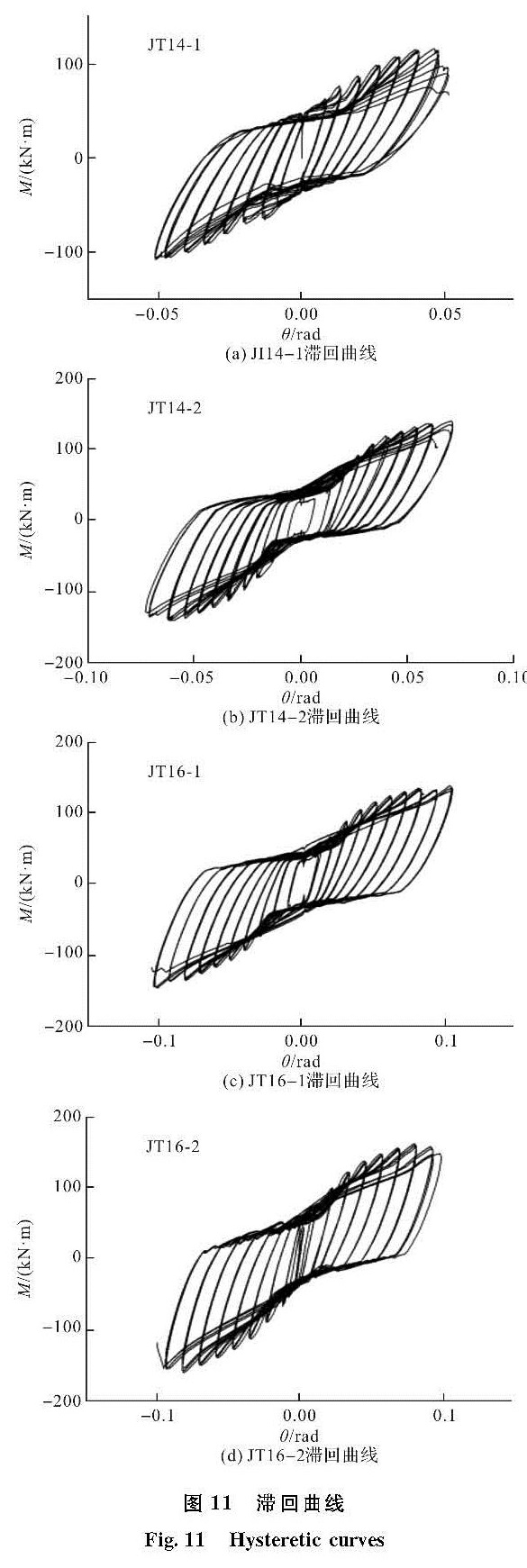
图 11为节点试验弯矩-转角的滞回曲线,反映结构在反复受力过程中的相关力学特性[15].从各曲线的形状来看,属于典型的反S形,出现较为严重的“捏缩”现象,这是因为构件中均采用摩擦性螺栓:(1)随着拉力的逐渐增大,螺栓的预紧力有所损耗,减小了螺栓与试件之间的摩擦力;(2)在反复加载过程中,螺栓与试件的接触面磨损,使得接触面变得光滑,从而减小了螺栓与试件之间的摩擦力,所以产生不同程度的滑移.在卸载阶段,螺栓反向受力而重新产生滑移回到初始位置,在此过程中,螺栓承载力很小,从而造成该阶段滞回曲线产生荷载急剧下降的小斜率滑移线段.实验的前中期,反复推拉三次加载过程中,残余变形很小,每一圈的滞回环基本重合.随着梁端位移的增大,螺栓产生滑移,使得每个滞回所吸收和耗散的能量逐渐增多,导致节点部位塑性变形区域不断的扩展,每一级的滞回环开始有所偏差.对比各图分析,T型件翼缘厚度的增加滞回饱和度无明显的变化,T型件加肋板之后,出现螺栓的滑移现象提早,导致滞回曲线的拐点出现较早.每一级的峰值来看,曲线的斜率逐渐有小幅度的减小,说明反复荷载作用下,节点的刚度开始有所退化.总体来说,四个构件的滞回曲线饱满度一般,刚度的退化不明显,表明此类节点的抗震性能和变形能力较好.
图 11 滞回曲线
Fig.11 Hysteretic curves
3.3 骨架曲线
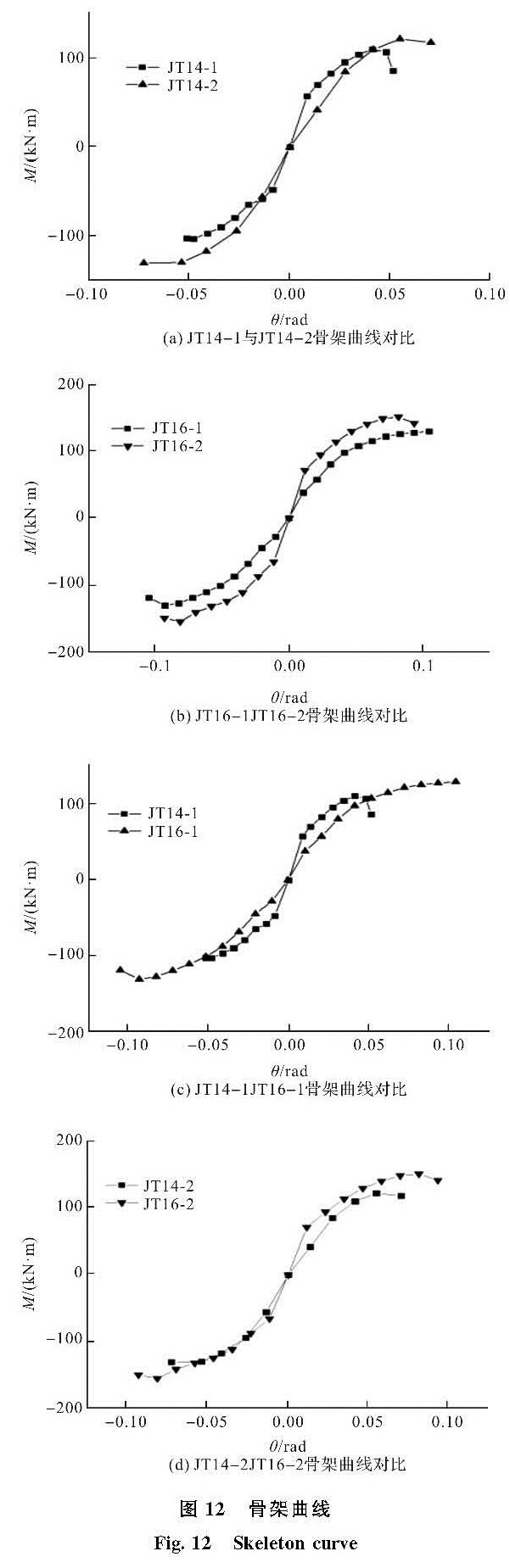
骨架曲线可以清晰的分析得出节点承载力的发展规律,图 12分别展示了不同构造参数T型件连接节点骨架曲线的两两对比情况.
图 12 骨架曲线
Fig.12 Skeleton curve
(1)图 12(a)为在T型件翼缘厚度为14的基础上加肋板的JT14-2和不加肋板的JT14-1曲线对比图,可以看出JT14-2的梁端极限位移和极限弯矩承载力要优于JT14-1,因为加肋板之后,节点的刚度得到提升,在同级位移加载下,JT14-2的斜率变化速度要比JT14-1缓慢.
(2)图 12(b)是在T型件翼缘厚度均为16 mm时不加肋板JT16-1和加肋板JT16-2两个骨架曲线的对比,很明显的可以观察到两曲线层次分明,在相同位移等级中,JT16-2的弯矩承载力都是要高于JT16-1的弯矩承载力.
(3)图 12(c)中为不同翼缘厚度的情况下,同时,不选择加肋板的两骨架曲线的对比图,JT14-1在破坏之前相同位移等级下,弯矩承载都是要高于JT16-1的,JT14-1在达到极限位移后,JT16-1继续试验直至破坏,最终结果来看JT16-1的极限弯矩承载力和极限位移均要大于JT14-1的极限弯矩承载力.
(4)图 12(d)为同时加肋板的条件不同翼缘厚度的两个骨架曲线对比,在正向加载阶段JT16-2的弯矩承载力均要高于JT14-2的弯矩承载力,而在负向加载阶段,构件在达到极限之前,有大部分曲线有所重叠.最后一级,达到最高点时,JT16-2的弯矩承载力和位移要明显超过JT14-2.
结合四个骨架曲线的对比分析,得出T型件在增大翼缘的厚度和增加肋板的情况下,梁柱节点弯矩承载力都有明显的提升.
3.4 刚度退化
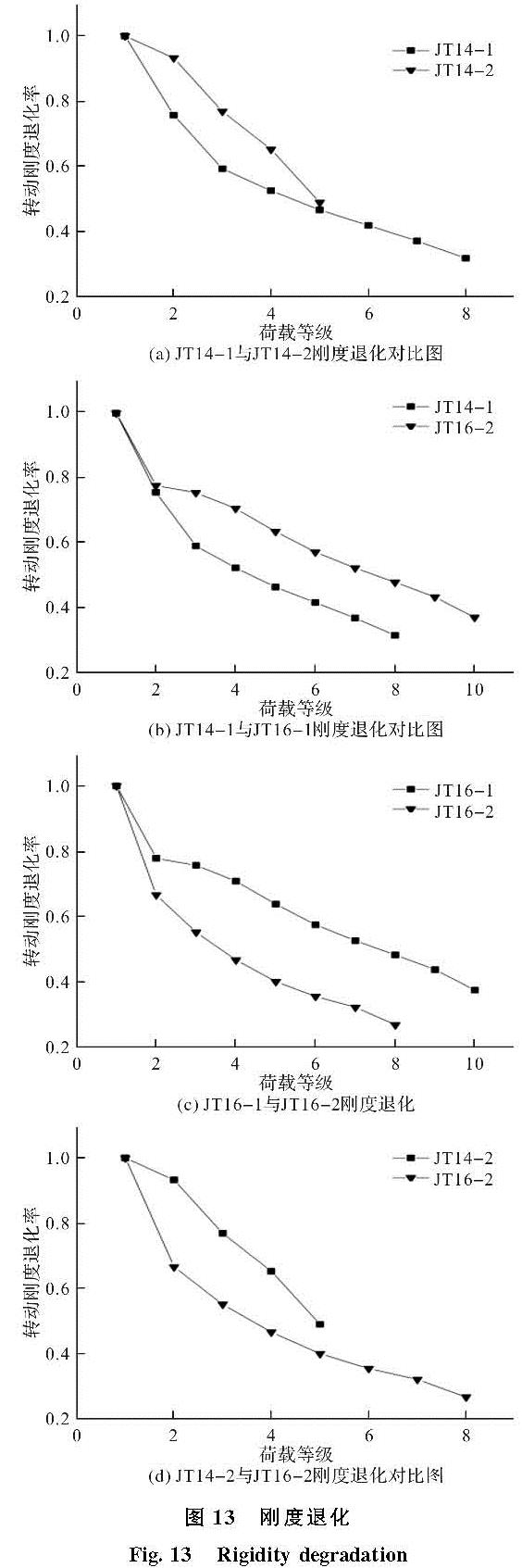
刚度退化作为评价结构抗震性能的重要指标,指构件刚度随着加载等级的增加而降低的特点,反应出构件的损伤程度[16].构件在进入塑性状态之后采用割线刚度来表述节点的转动刚度,用计算公式(1)来确定数值成表4,图 13为各构件节点转动刚度退化率-荷载等级相互对比图.
Ki=(|+Mi|+|-Mi|)/(|+θi|+|-θi|) (1)
式中:Ki为节点的弯矩转动刚度; Mi为某一级荷载作用下弯矩承载力峰值; θi某一级荷载作用下弯矩承载力峰值对应的转角; 正负号为加载方向,推为正,拉为负.
图 13 刚度退化
Fig.13 Rigidity degradation
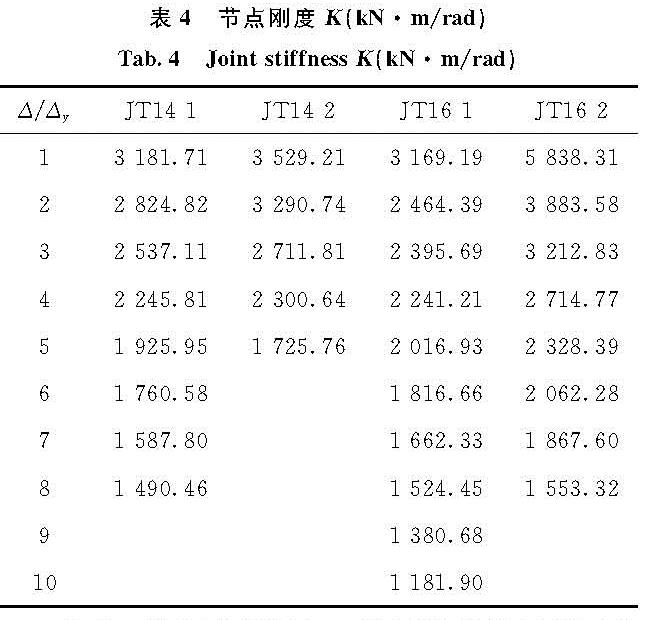
表4 节点刚度 K(kN·m/rad)
Tab.4 Joint stiffness K(kN·m/rad)
从表4数据分析得知,T型件翼缘厚度同为14 mm时,加肋板的JT14-2与不加肋板的JT14-1相比较初始转动刚度提升了10.92%; 翼缘厚度为16 mm加肋板后,JT16-2的初始转动刚度有很明显的增大,提升了84.22%; 在不加肋板的情况下,只增加T型件翼缘厚度,JT14-1的初始转动刚度相比较于JT16-1几乎没有什么变化,说明在不加肋板时,翼缘的厚度对构件的转动刚度影响很小.但在同时加肋板后,JT16-2相比较JT14-2的初始转动刚度增加了65.43%,表明加肋板后T型件的增强,使得整个构件的刚度有大幅度的提升.
图 13为转动刚度退化率-荷载等级示意图,表现试件在每一级的变化,图 13(a)、(d)JT14-2相比JT14-1、JT16-2下降速度明显要迅速,图 13(b)、13(c)中JT16-1相比较JT14-1和JT16-2初期有一重叠段,随着荷载等级的增加刚度退化下降速度逐渐加快.通过分析可知T型件的翼缘厚度对节点刚度提升影响不大,在T型件上加肋板后,初始转动刚度变化有明显加强.
3.5 延性和耗能能力
在节点试验中,采用转角延性进行分析,延性系数越大表示其构件在地震作用下变形能力便越强、耗散地震的能量越多,计算公式为(2).
μθ=θu/θy (2)
式中:θu为节点破坏时的转角; θy为节点屈服时的转角.
耗能能力采用等效黏滞阻尼系数he,能量耗散系数E及试验总耗能来表示,he的值越大说明结构的耗能能力越好,结构的抗震性能越好,由公式(3)和(4)分别来计算he、E,四个试验计算结果见表(5)所示.
e=1/(2π)(S(ABC+CDA))/(S(OBE+ODF)) (3)
E=(S(ABC+CDA))/(S(OBE+ODF)) (4)
式中:S(ABC+CDA)为滞回圈ABCD的面积; S(OBE)为三角形OBD的面积; S(ODF)为三角形ODF的面积.
图 14 等效粘滞阻尼系数he计算简图
Fig.14 Calculation diagram of equivalent viscous damping coefficient he
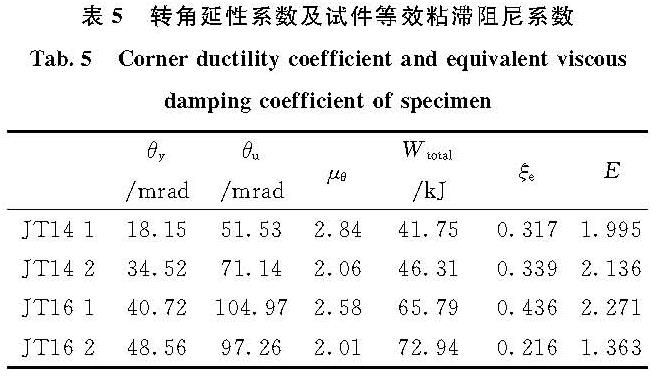
从表(5)中数据分析得出,每一个节点试验的转角延性系数表现良好,数值均在2~3之间,说明四个构件都具备良好的变形能力.具体分析来看:
(1)在T型件上加肋板后,JT14-2和JT16-2的转角延性系数要小于不加肋板的JT14-1和JT16-1,延性系数分别下降了27.46%和22.09%,说明在T型件加肋板后,T型件的刚度有所提升,使得在试验过程中变形能力相对有所下降.增加T型件翼缘的厚度对构件的延性系数影响不大,JT16-1延性系数比JT14-1减小了9.15%,JT16-2比JT14-2减小了2.43%;
(2)在T型件翼缘厚度同为14 mm的情况下加肋对整个构件有一定的影响,加肋的JT14-2与不加肋板的JT14-1等效黏滞阻尼系数及能量耗散系数分别提升了6.94%、7.08%; 当都不加肋板的条件下增加T型件的厚度JT16-1相较于JT14-1等效黏滞阻尼系数和能量耗散系数同样有显著的提高,分别为37.54%、13.83%.在增加翼缘厚度的同时又加肋板试件JT16-2的耗能能力表现稍差,相对于同厚度不加肋板的JT16-1和不同厚度加肋板的JT14-2,不但没有所增加反而有明显下降,等效黏滞阻尼系数分别减小了50.46%、36.28%,能量耗散系数下降了39.98%和36.19%.其主要原因有两点:1)不管翼缘的厚度增加还是加肋板都是加强了T型件的刚度,构件变形能力有所下降,在实验过程中,使得螺栓的滑移提前发生,加剧滑移的程度; 2)肋板是后期人工在原有的T型件上附加焊接,在翼缘的厚度由14增加到16后T型件的自身刚度有所提升,而加肋板的焊缝的塑性变形能力较差,从而导致JT16-2的整体耗能能力急剧减弱.
表5 转角延性系数及试件等效粘滞阻尼系数
Tab.5 Corner ductility coefficient and equivalent viscous damping coefficient of specimen