基金项目:国家自然科学基金项目(51408453); 陕西省自然科学基础研究计划项目(2020JM-475); 西安市科技创新人才服务企业项目(2020KJRC0047)
第一作者:孙建鹏(1981—),男,博士,副教授,研究方向为新型桥梁结构分析及抗震、工程结构防灾减灾.E-mail:sunjianpeng2001@163.com 通信作者:黄文锋(1982—),男,博士,副教授,研究方向为结构风振相应分析、风灾危险性分析.E-mail:wfhuang@hfut.edu.cn
(1.西安建筑科技大学 土木工程学院,陕西 西安 710055; 2.合肥工业大学 土木工程学院,安徽 合肥,230009; 3.中国铁建大桥工程局集团有限公司,天津 300300; 4.中铁建大桥工程局集团第四工程有限公司,黑龙江 哈尔滨 150000)
(1.School of Civil Engineering, Xi'an Univ. of Arch.& Tech., Xi'an 710055, China; 2.School of Civil Engineering, Hefei University of Technology, Hefei 230009, China; 3.China Railway Construction Bridge Engineering Bureau Group Co., Ltd., Tianjin 300300, China; 4.China Railway Construction Bridge Engineering Bureau Group Fourth Engineering Co., Ltd., Harbin 150000, China)
atmospheric environment; typhoon extreme wind speed; typhoon key parameters; numerical simulation
DOI: 10.15986/j.1006-7930.2023.03.004
中国地处亚洲东部,西北与亚欧大陆接壤,东南与太平洋毗邻,在拥有960万 km2领土的同时,也有着300万km2领海.在我国拥有的将近3.2万km的海岸线中,主要分布在我国的东南沿海地区.有记录显示,每年登陆我国的台风将有8个之多,而2021年7月的台风‘烟花'足足在我国内陆停留了95 h之久,造成了极大的经济损失和人员伤亡.台风作为极为频繁的自然灾害,对我国的东南沿海城市造成了极为严重的经济损失.因此,对我国东南沿海城市进行台风极值风速研究极其重要.
事实上,目前对于台风极值风速研究的方法主要为模拟圆法[1-2]和台风的合成路径模拟方法[3-4].模拟圆法首先利用台风历史数据资料确定台风关键参数的概率分布,然后利用Monte Carlo模拟进行大量抽样,结合台风模型进行足够多次数的台风模拟.由于此方法操作方便,得到了众多学者的广泛使用和发展[5-6].然而,该方法需要有大量的台风历史观测数据才能有着较好的模拟效果,因此对于历史观测数据较少的地区模拟效果误差较大.为了解决模拟圆法存在的不足,VICKERY等[4]2000年提出了台风的合成路径模拟方法,该方法通常由起点模型、路径模型和强度模型模拟台风从生成到消亡的台风全寿命周期.之后,大量的国内外学者对其进行改进与发展,并利用各种改进后的模型进行了台风极值风速的研究.自此之后,有很多学者针对台风危险性分析做了大量研究,LI和HONG[7]对VICKERY等提出的方法利用回归加权进行了改进,并验证该模型的可靠性.肖玉凤等[9]通过调整中国东南沿海地区最大风速半径的计算方法来提高计算精度.刘大伟[8]则是利用路径分类的方法将台风路径分为5类,对该5类的台风路径分别进行研究,来提高台风极值风速计算的准确性.姚博等[10]则通过考虑地区的混合气候来改进台风极值风速研究方法.王宁娟[11]通过对CE风场的改进来提高对中国东南沿海台风的模拟精度.吴甜甜[12]通过构建阻滞增长模型对台风的强度模型进行改进.虽然以上方法的模拟精度相比于以往的台风研究方法有了一定的提高,但是其并没有解决对台风历史数据的依赖性这个问题.对于那些历史观测数据较少,但存在较大台风发生概率的地区,该方法同样模拟误差较大.
现如今,全球气候变化日益加剧,气候的变化不仅对室内设计条件、建筑物使用条件等有着较大的影响,而且对自然灾害的发生也有着极为关键的影响[13].国内外学者做了许多研究发现,台风的发生以及强度与大气环境的改变有着较大的关联.GARY等[14]首先提出了关于大气海洋环境的经验生成指数,并被不断的发展完善.随后EMANUEL和NOLAN[15]为了解决GARY的经验指数无法适应气候变化缺点,对GARY经验指数进行了适当的改进,提出了台风潜在生成指数(Genesis Potential Index, GPI),而TIPPETT[16]为了降低模型计算的复杂性,利用海平面温度代替了GPI中的潜在强度.中国学者赵军平[17]则是利用GPI针对南海海域以及西北太平洋海域进行了特定的改进,提升了GPI的模拟效果.KNUTSON等[18]对大西洋热带气旋活动进行了研究,研究发现在全球大气环境的变化下,20世纪后期热带气旋的发生频次有着一定幅度的下降.MURAKAMI等[19]为了研究全球气候变化下的热带气旋活动,利用日本气象研究所的大气环流模式研究发现20世纪70年代后的台风发生总数有着明显的降低,而不同的海域有着不同的变化形式,西北太平洋和南太平洋有所降低,中太平洋将有所增长.尽管以上研究表明在全球气候变化下,台风的发生数量有所减少,但是MEI等[20]研究发现,由于海水表面温度提高以及一些其他大气环境的变化,导致强台风的发生频次大大增加.钟维军等[21]利用统计确定性模型并结合4种不同的预测模型对全球气候变化对台风极值风速的影响进行了研究,研究发现未来台风极值风速可能超过20世纪末,并且在重现期100 a下的台风极值风速呈增长趋势.
为了考虑全球环境变化对台风的影响,并且摆脱台风模拟对历史观测数据的影响,本文将采用由大气环境参数构成的台风模型,并以香港地区为研究对象台风极值风速进行计算,同时将其与历史观测数据结果进行比较分析,从而验证模型的有效性.
台风的生成与发展是一个极为复杂的过程,期间受到很多大气环境参数的影响,例如海洋表面温度、涡度、湿度、垂直风切等等.为了能够充分考虑大气环境参数对台风的影响,本文将采用起点模型、路径模型以及强度模型对台风的全寿命周期进行模拟.本研究全过程采用MATLAB编程进行数值模拟,利用大气环境参数对台风的生成与发展进行分析预测.
台风的起点模型对于台风合成路径模型起着至关重要的作用,它是模拟一个台风全路径的起点,只有确定一个较为准确的起点位置及起点个数,才能确保台风在行进过程中能有一个较好的行进路线,从而才能确保一个台风的成功模拟.以往台风起点模型多采用三维高斯核密度函数对台风历史起点数据进行拟合得到台风起点时空概率分布模型[21-22],而本文将采用Tippett等[16]提出的热带气旋生成指数(TCGI)对西北太平洋地区的台风起点数量进行模拟,同时利用TCGI对每个台风位置和时间进行随机分配,从而形成一个完整的台风模型.具体实现方法如下所示.
泊松分布被常常应用在统计数据的建模中,假如随机变量N满足泊松分布,设N=0,1,2,…,则有概率
P(N=n)=e-μμn/n! (1)
式中:N是台风起点数量.台风起点预测期望值是通过气候变量的向量x得到.由于预测期望值μ线性依赖于气候变量x会使得μ出现负值,因此通过对数线性模型来解决这个问题,其中log(μ)与变量x是线性相关的,即
log(μ)=bTx (2)
式中,b是系数的向量,上式也可转换为
μ=exp(bTx) (3)
气候变量和台风起点历史数据都被定义在2.5°×2.5°网格中.为了能够更好的区分不同纬度的区域不同,将公式3修改为
μ=exp(bTx+log(cosφ)) (4)
式中:φ为纬度.log(cosφ)的系数为1,使得单位指数bTx代表每个区域的台风起点数量.
本文将利用Tippett[16]在2011年提出的TCGI起点模型,对台风的起点进行模拟,具体公式如下.
TCGI=exp(b+bηη850+brhRH600+bsstSSTR+bshrdSHRD+log(cosφ)) (5)
式中:TCGI为起点数量的期望值; η850,RH600,SSTR和SHRD分别是850 hPa的绝对涡度,600 hPa的相对湿度,相对海平面温度(SST相对于热带平均SST)和850和200 hPa之间的垂直风切; b是截距,bx是变量x相对应的系数; φ为纬度.利用1961~2000年的40年台风历史起点数据和气象数据在2.5°×2.5°网格下对公式5进行拟合得到截距b和系数bx.
本文路径模型采用Marks[23]在1992年提出的β漂流模型(BAM),BAM结合了Li 和 Wang[24]在1994年提出的β漂流和基于大尺度低层(850 hPa)以及高层(250 hPa)风线性组合的平均平流为
V=aV850+bV250+Vβ (6)
式中,V850和V250是850 hPa和250 hPa两个气压层纬向风(u)和经向风(v)时间序列的矢量和; a、b是两个气压层加权系数,其中a+b=1; Vβ是β漂流项,Vβ=[uβ,vβ].
(dx)/(dt)=V (7)
产生台风起点数量和起点位置后,路径模型将以1 h为步长向前推进台风.本研究只研究西北太平洋地区,即东经80°到西经120°,北纬0°到北纬70°之间的海域.超出此区域的,台风将自动终止.
对于台风动力路径模型公式6,我们取a=0.8,则b=0.2,同时Vβ=[2.5cosθ,1.0cosθ ],θ为纬度.V的组成由下列公式表示,即
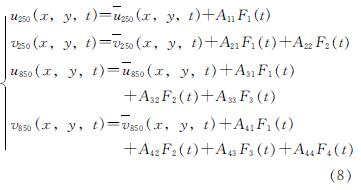
式中:u^-和v^-是根据月平均场线性插值得到的日分辨率风; Fi(t)(i=1,2,3,4)是具有随机相位的傅里叶级数变量,用其来表示小于月的时间尺度的风的随机性[25. Fi(t)表示为
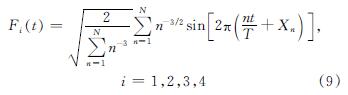
式中:T是时间序列中的最低频率(15 d); N为总波数,这里取10,Xn是均匀分布在0和1之间的随机数; Ai,j是下三角矩阵A第i行,第j列的元素,A矩阵满足
ATA=cov (10)
式(9)中采用n-3/2来对观测到的地转湍流谱进行模拟,那是因为合成风动能的功率谱接近频率的立方倒数.总而言之,利用公式(8)和公式(10)可得到850 hPa和250 hPa的合成风,其月平均值、方差和协方差与再分析数据集中的一致.
台风移动过程中,除了起点以外的其他各点强度与其前一步的强度有着很大的关联性,我们都可以用前一步台风强度计算得到当前步的台风强度,因此,本文将利用相对强度的自回归模型来表示台风强度的变化,公式如下.
ln(IRi+1=α1+α2ln(IRi+α3SSTi+α4(SSTi+1+SSTi)+ε (11)
式中:α1,α2,α3,α4为模型中的参数; IR为相对强度,计算公式见公式(12); SST为海平面温度; ε为在2.5°×2.5°分辨率下,每个网格的平均误差.
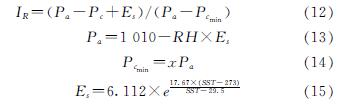
式中:Pa为外围气压; Pc为中心气压; Es为饱和蒸汽压; Pcmin为中心气压最小表面值; RH为相对湿度.x为Pa和Pcmin之间的系数,其可以由公式(16)计算得到.
ln(x)=-A[1/x-B] (16)
具体的推导公式Emanuel在文献[26]给出.
台风风场模型在台风极值风速预测中起着极其重要的作用,它将直接影响到台风极值风速预测的精确度.Yan Meng[27]台风风场模型有着较高的计算效率和准确性,因此本文采用Yan Meng台风风场模型.
Yan Meng台风风场模型的模型基本理论形式如下所示.
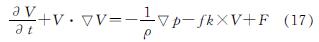
式中:V为台风风速,V=VG+VF,VG代表梯度风速,如公式(18),VF代表地表摩擦阻力风速,如公式(19); F为科式力系数; f为代表摩擦阻力; ρ为空气密度; 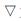 为二维倒数算子符号,
为二维倒数算子符号,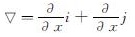 ; P为Holland气压,如公式(20)表示.
; P为Holland气压,如公式(20)表示.
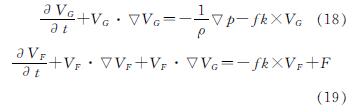
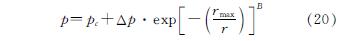
式中:Pc为台风中心气压,hPa; Δp为台风中心气压差,hPa; rmax为台风最大风速半径,km; r为到台风中心的距离,km; B为Holland气压参数,计算公式如下.
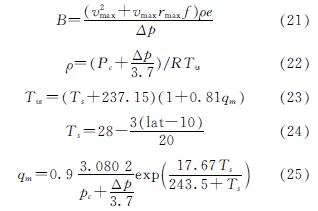
式中:vmax为台风最大风速,m/s; e为欧拉常数,通常取2.718; R为普适气体常数,通常取286.9 J·K·mol; Tvs为虚表面温度,K; Ts为空气表面温度,K; qm为蒸气压(相对湿度90%); lat为纬度.
本文将以香港为研究对象,利用本文的方法对该地区的大气环境变化下的台风进行模拟,并对未来不同重现期下的台风极值风速进行计算.本文将采用的天台风历史观测数据来自于中国台风网,大气环境数据来自于欧洲中期天气预报中心(ERA-Interim)再分析数据集,该数据集记录了1979年到2019年的相关大气海洋环境数据.
为了能够准确地描述出台风的特征等级,国内外学者一般采用台风关键参数对台风进行描述,目前常见的台风关键参数有台风中心气压差Δp、台风移动速度c、台风移动方向θ、台风最小距离dmin以及台风最大风速半径rmax等.利用上述台风模型对香港地区的台风关键参数并计算并绘制直方图如下图1所示.
为了能够更加理性的分析台风各关键参数模拟的可靠性,本文将会利用χ2检验法和K-S检验法对台风关键参数的模拟效果进行检验.
χ2检验法:
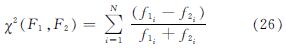
K-S检验法:
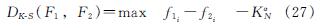
上式中,F1和F2为历史观测数据和模拟结果的直方图; N为直方图所分的组数,KαN=1.36/N1/2; f1i和f2i为历史观测数据和模拟结果的直方图在第i组的频率; max|f1i-f2i|为历史观测与模拟结果差值绝对值的最大值.
当计算得到的χ2越大,说明历史观测数据和模拟结果的误差较大; χ2越小说明历史观测数据和模拟结果的误差较小; 若χ2等于0,这表明历史观测数据和模拟结果完全吻合.DK-S(F1,F2)为历史观测与模拟结果差值绝对值的最大值与KαN的差值,若DK-S(F1,F2)大于零,则历史观测与模拟结果的误差较大; DK-S(F1,F2)小于零,则历史观测与模拟结果的误差较小.检验结果如下表所示.
表1 χ2检验法和K-S检验法检验数值
Tab.1 Chi-square test and K-S test for testing values
通过将香港地区的历史观测数据的台风关键参数与模拟路径的台风关键参数数据进行对比发现,模拟得到的结果与历史观测数据非常相似,验证了台风路径模型的可靠性.香港地区台风关键参数经过χ2检验值均不大于0.09,可以推断出由模拟路径提取得到的台风关键参数与台风历史路径的台风关键参数有着较小的误差,模拟效果较好; K-S检验法得到的香港地区的台风关键词参数检验值均小于0,亦可知模拟路径得到台风关键参数与历史路径的台风关键参数的误差较小.
将获得的台风关键参数结合台风风场模型获得台风在200 m高度和梯度风高度的台风风速和风向,从而结合台风年发生率计算得到台风的最大风速序列,并利用极值I型(Gumbel)分布公式(28)计算得到台风在不同重现期下的台风极值风速.
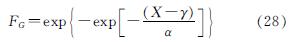
式中:α尺度参数; β形状参数; γ位置参数.
台风风速的重现期是对台风极值风速预测很重要的数据,它是指每T年内发生一次台风最大风速v大于在一定范围内(通常取模拟圆半径250 km)某一台风路径在特定研究点的最大风速值VT,那么就称时间T为最大风速值VT的重现期.
如果在一个台风行进过程中,台风最大风速V小于某一特定风速v的概率记为Fv,这在n个台风行进过程中,每一个台风最大风速V小于某一特定风速v的概率可记为
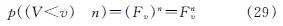
τ年内,每一个台风最大风速V小于某一特定风速v的概率可记为
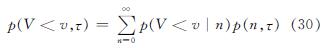
如果某一台风研究点的年发生率λ满足参数为λ的泊松分布,则将公式(29)和公式(30)相结合即可得到公式为
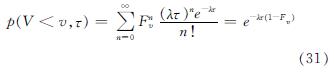
为了得到任意一年内每一个台风最大风速V小于某一特定风速v的概率,我们取τ为1,即可得到
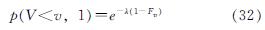
又因为重现期为T时,任意一年内每一个台风最大风速V小于某一特定风速v的概率为
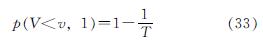
将公式(32)和公式(33)相结合即可得到
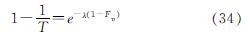
利用模拟获得m次台风路径,将每次模拟台风过程的最大风速进行由小到大排列,即可得到模拟台风的最大风速序列,记为v1,v1,…,vi,…,vm.取其中任一风速vi,则在整个台风移动过程,任意时刻的台风风速U小于vi的概率可记为
Fvi=i/(m+1) (35)
将公式(35)代入公式(34)即可得:
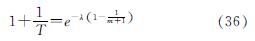
将公式(36)等号两边同时取对数并变形可得重新期T为

则重现期T下的台风最大风速为
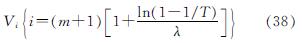
将公式(36)和公式(38)与台风极值风速概率分布结合,可得到重现期T下的台风最大分速Vi为
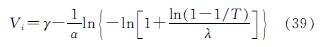
利用上述方法即可计算得到香港地区在20 a、50 a、100 a以及200 a重现期下的台风极值风速,并将历史数据计算结果与模拟计算结果进行对比,对比结果如图2和表2.
从图2看出,历史路径和模拟路径的台风风速概率分布较为一致; 从表2可以看出,利用模拟路径得到的香港地区的台风在不同重现期下的极值风速要大于历史路径模拟得到的台风极值风速,在200 m高度和梯度高度下,差值最大分别可达1.389 8 m/s和3.807 8 m/s,由于本文的台风模型是利用海洋大气环境因素所构成的,因此随着全球的气候变暖,不仅超强台风的发生率会有一定的提升,而且每次台风的强度也会有着不同程度的增强,主要体现在台风极值风速的提高; 相反利用历史路径对台风极值风速进行模拟则是对以往的台风极值风速的模拟,无法对台风未来的发生率以及台风极值风速做出准确的预测,也无法更好的考虑到大气环境变化对台风的影响,而且利用历史路径对台风极值风速的模拟结果与模拟路径的模拟结果的差值会随着重现期的不断增大会不断地增大.
主要对中国香港地区的台风极值风速进行计算.利用考虑大气环境的台风模型,其中包括起点模型、路径模型以及强度模型,模拟得到若干个台风路径,从而得到各个台风路径的台风关键参数; 然后将台风关键参数带入台风模型并结合台风年发生率和极值Ⅰ型(Gumbel)分布计算得到台风在不同重现期下的台风极值风速.将本研究的计算结果与历史数据进行对比,得到以下结论:
(1)考虑大气环境的台风模型对台风关键参数的模拟结果与历史数据结果有着较高的相似度,表明了考虑大气环境的台风模型的可靠性;
(2)模拟得到的台风风速概率分布与历史观测结果相似度较高; 模拟路径不同重现期下的极值风速要大于历史路径台风极值风速,在200 m高度和梯度高度下,差值最大分别可达1.39 m/s和3.81 m/s.由于台风模型是利用海洋大气环境因素所构成的,因此随着全球的气候变暖,不仅超强台风的发生率会有一定的提升,而且每次台风的强度也会有着不同程度的增强,主要体现在台风极值风速的提高.